
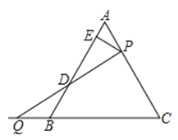
【题目】如图,△ABC 是边长为 6 cm 的等边三角形,P 从点 A 岀发沿 AC 边向 C 运动, 与此同时 Q 从 B 出发以相同的速度沿 CB 延长线方向运动.当 P 到达 C 点时,P、Q 停止运动, 连接 PQ 交 AB 于 D
(1)设 P、Q 的运动速度为 1 cm/s,当运动时间为多少时,∠BQD=30°?
(2)过 P 作 PE⊥AB 于 E,在运动过程中线段 ED 的长是否发生变化?如果不变,求出线段 ED的长;如果变化请说明理由
【答案】(1) 运动时间为2s;(2) ED 的长不会发生变化,DE=3.
【解析】
(1) 根据三角形内角和为180![]() , 可知△PQC为直角三角形, 根据特殊角的三角函数值即可求出AP的长后可得时间.
, 可知△PQC为直角三角形, 根据特殊角的三角函数值即可求出AP的长后可得时间.
(2) 根据全等三角形的角角边判定定理可得,Rt△ABE≌Rt△BQF,再由全等三角形对应边相等可知:AE=BF,EP=QF, 因为EP//QF, 可知四边形EPFQ是平行四边形, 根据平行四边形对角线互相平分可得: DE=![]() EF.EB+AE=BE+BF=AB,DE=
EF.EB+AE=BE+BF=AB,DE=![]() AB., 由于△ABC是不变的, AB是定长, 即可证明当点P、 Q运动时, 线段DE的长度不会改变.
AB., 由于△ABC是不变的, AB是定长, 即可证明当点P、 Q运动时, 线段DE的长度不会改变.
解:(1)![]() △ABC是边长为6的等边三角形,
△ABC是边长为6的等边三角形,![]() ∠ACB=60
∠ACB=60![]() .
.
![]() ∠BQD=30
∠BQD=30![]() ,
,![]() ∠QPC=90
∠QPC=90![]() .
.
设AP=x,则PC=6-x,QB=x,
![]() QC=QB+BC=6+x,PC=AC-AP=6-x,
QC=QB+BC=6+x,PC=AC-AP=6-x,
在Rt△QCP中, ∠BQD=30![]() ,
,
PC=![]() QC,即6-x=
QC,即6-x=![]() (6+x),
(6+x),
解得x=2,
又![]() P、Q 的运动速度为 1 cm/s,
P、Q 的运动速度为 1 cm/s,
![]() 运动的时间为2s;
运动的时间为2s;
(2) 当点P、 Q运动时, 线段ED的长度不会改变.理由如下:作QF⊥AB, 交直线AB的延长线于点F,连接QE,PF.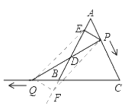
![]() PE⊥AB于E,
PE⊥AB于E,![]() ∠DFQ=∠AEP=90
∠DFQ=∠AEP=90![]() .
.
![]() 点P、Q做匀速运动且速度相同,
点P、Q做匀速运动且速度相同,![]() AP=BQ.
AP=BQ.
![]() △ABC是等边三角形,
△ABC是等边三角形,
![]() ∠A=∠ABC=∠FBQ=60
∠A=∠ABC=∠FBQ=60![]() .
.
![]() 在△APE和△BQF中,
在△APE和△BQF中,
![]() ∠A=∠FBQ,AP=BQ,∠AEP=∠BFQ=90
∠A=∠FBQ,AP=BQ,∠AEP=∠BFQ=90![]() ,
,
![]() △APE≌△BQF (AAS).
△APE≌△BQF (AAS).
![]() AE=BF,PE=QF且PE∥QF.
AE=BF,PE=QF且PE∥QF.
![]() 四边形PEQF是平行四边形。
四边形PEQF是平行四边形。
![]() DE=
DE=![]() EF.
EF.
![]() EB+AE=BE+BF=AB,
EB+AE=BE+BF=AB,
![]() DE=
DE=![]() AB.
AB.
又![]() 等边△ABC的边长为6,
等边△ABC的边长为6, ![]() DE=3.
DE=3.
![]() 当点P、Q运动时, 线段ED的长度不会改变.
当点P、Q运动时, 线段ED的长度不会改变.


科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程![]() 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?
经过小组交流讨论后,同学们逐渐形成了两种意见:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.由题意可得a﹣2>0,所以a>2,问题解决.
小强说:你考虑的不全面.还必须保证a≠3才行.
老师说:小强所说完全正确.
请回答:小明考虑问题不全面,主要体现在哪里?请你简要说明: .
完成下列问题:
(1)已知关于x的方程![]() =1的解为负数,求m的取值范围;
=1的解为负数,求m的取值范围;
(2)若关于x的分式方程![]() =﹣1无解.直接写出n的取值范围.
=﹣1无解.直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF的各顶点分别在双曲线y= ![]() ,y=
,y= ![]() ,y=
,y= ![]() 在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC﹣S△DEF=( )
在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC﹣S△DEF=( ) 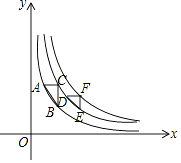
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形纸片 ABC 中,∠ACB=90°,AC≤BC.如图,将纸片沿某条直线折叠,使点 A 落在直角边 BC 上,记落点为 D.设折痕与 AB、AC 边分别交于点 E、点 F,当折叠后的△CDF 与△BDE 均为等腰三角形,那么纸片中∠B 的度数是_____
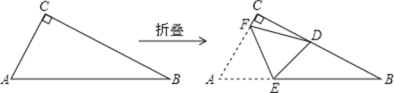
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村建设前,某乡在一条笔直的公路旁依次有A、B、D、E、F五个村庄(每相邻两个村庄之间有农田).后来由于新农村建设需要,在该公路旁新建了C庄,已知C庄在A庄和F庄之间,B庄是A庄和C庄的中点,E庄是C庄和F庄的中点,D庄是B庄和E庄的中点.
(1)按题意画出大致示意图;
(2)若A庄和C庄相距4千米,C庄和F庄相距12千米,求C庄和D庄之间的距离;
(3)若A庄和F庄之间的距离是C庄和D庄之间距离的8倍,求A庄和C庄之间的距离与C庄和F庄之间的距离的比值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com