
若m2-2m=1,则2m2-4m+2007的值是________.
|
分析:要求代数式的值,若能求出m的具体值,问题即可解决.但运用现在已学的知识无法根据已知条件求得m的值.观察已知条件和待求式的特点,若先将2m2-4m+2007逆用乘法的分配律进行适当的变形,使之逼近已知条件,再利用整体代入便可求值,这样既简捷,又准确. 解:因为2m2-4m+2007=2(m2-2m)+2007, 将m2-2m=1整体代入,得原式=2×1+2007=2009. 点评:一般地,求代数式的值有两种常见的类型:一是给定一个代数式及字母的值,求这个代数式的值,此时直接将字母的值代入计算即可;二是给定一个代数式和它的值,求另一个代数式的值,此时应把待求式向有利于求值的方向转化,直至能求出其值(如本例). |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:双色笔记八年级数学上(北京师大版) 题型:013
若一次函数y=2mx+(m2-2m)的图像经过坐标原点,则
[ ]
查看答案和解析>>
科目:初中数学 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:013
若二次函数y=(m+1)x2+m2-2m-3的图象经过原点,则m的值必为
A.-1或3
B.-1
C.3
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
⑴图②中的阴影部分的面积为 ;
⑵观察图②请你写出三个代数式(m+n)2、(m-n)2、mn之间的等量关系是
.
⑶若x+y=-6,xy=2.75,则x-y= .
⑷实际上有许多代数恒等式可以用图形的面积来表示.
如图③,它表示了 .
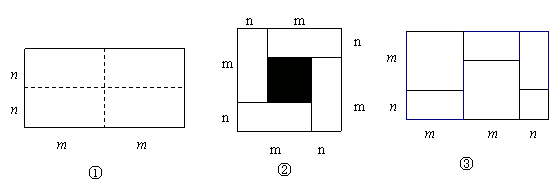
⑸试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com