
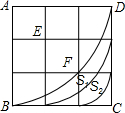
 如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.
如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3. 分析 根据已知图形分别利用S1=5+S扇形EMN-S扇形ABD,S2=3+S扇形FPQ-S扇形EMN,进而得出答案.
解答  解:∵S扇形ABD=$\frac{90}{360}$π×32=$\frac{9}{4}$π,S扇形FPQ=$\frac{π}{4}$,S扇形EMN$\frac{90π×{2}^{2}}{360}$=π,
解:∵S扇形ABD=$\frac{90}{360}$π×32=$\frac{9}{4}$π,S扇形FPQ=$\frac{π}{4}$,S扇形EMN$\frac{90π×{2}^{2}}{360}$=π,
∴S1=5+S扇形EMN-S扇形ABD=5+$\frac{90π×{2}^{2}}{360}$-$\frac{9}{4}$π=5(1-$\frac{π}{4}$),
同理可得:S2=3+S扇形FPQ-S扇形EMN
=3+$\frac{π}{4}$-π
=3(1-$\frac{π}{4}$),
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5(1-\frac{π}{4})}{3(1-\frac{π}{4})}$=$\frac{5}{3}$.
故答案为:5:3.
点评 此题主要考查了扇形面积的计算,正确记忆扇形面积求法分别表示出S1,S2的值是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我国二炮部队一批导弹的杀伤半径 | |
| B. | 了解中央电视台CCTV4《今日关注》栏目的收视率 | |
| C. | 了解射阳河流域中鱼的种类 | |
| D. | “勿忘国耻、振兴中华”!了解某班学生对我国政府设立“南京大屠杀国家公祭日”的知晓率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com