
���� ��1��С���Ѿ�����������Ϊ4����С��4�Ľ��Ϊ4��2������4�Ľ����Ϊ4��10��Ȼ����ݸ��ʹ�ʽ��⣻
��2��С���Ѿ�����������Ϊ2����С��2�Ľ��Ϊ0������2�Ľ����Ϊ4��12��Ȼ����ݸ��ʹ�ʽ��⣻С���Ѿ�����������ΪA����С��A�Ľ��Ϊ4��12������2�Ľ����Ϊ0��Ȼ����ݸ��ʹ�ʽ��⣮
��� �⣺��1����Ϊһ���˿�ȥ����С������4��13=52���ƣ�
��С���Ѿ�������������4�����С����ʤ�Ļ���Сӱֻ����������������2����3��
���ԣ�С����ʤ�ĸ�����$\frac{2��4}{51}=\frac{8}{51}$��
���СӱҪ��ʤ������������ֻ����5��6��7��8��9��10��J��Q��K��A��
���ԣ�Сӱ��ʤ�ĸ�����$\frac{4��10}{51}=\frac{40}{51}$��
��2����С���Ѿ�����������Ϊ2��
��ôС����ʤ�ĸ�����0��Сӱ��ʤ�ĸ�����$\frac{4��12}{51}=\frac{48}{51}$��
��С���Ѿ�����������ΪA��
��ôС����ʤ�ĸ�����$\frac{4��12}{51}=\frac{48}{51}$��Сӱ��ʤ�ĸ�����0��
���� ���⿼�����б�������״ͼ���������б�������״ͼ��չʾ���еȿ��ܵĽ��n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��Ȼ�����ø��ʹ�ʽ�����¼�A���¼�B�ĸ��ʣ�Ҳ�����˸��ʹ�ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
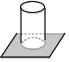 ��ͼ��һ��������ˮƽ�����ϵ�Բ���������濴����ͼ���ǣ�������
��ͼ��һ��������ˮƽ�����ϵ�Բ���������濴����ͼ���ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2��3 | B�� | 1��3��5 | C�� | 4��5��6 | D�� | 3��4��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������ABCD�ĸ�AE��EΪCD���е㣮AE=$\sqrt{3}$cm��������ABCD���ܳ��ǣ�������
��ͼ��������ABCD�ĸ�AE��EΪCD���е㣮AE=$\sqrt{3}$cm��������ABCD���ܳ��ǣ�������| A�� | 4$\sqrt{3}$cm | B�� | 4$\sqrt{2}$cm | C�� | 4cm | D�� | 8cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ODC���ɡ�OAB�Ƶ�O˳ʱ����ת30���õ���ͼ�Σ�����Dǡ������AB�ϣ����BDC�Ķ�����30�㣮
��ͼ����ODC���ɡ�OAB�Ƶ�O˳ʱ����ת30���õ���ͼ�Σ�����Dǡ������AB�ϣ����BDC�Ķ�����30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
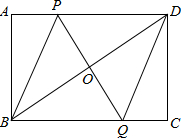 ��ͼ���ھ���ABCD�У�P��AD��һ���㣬OΪBD���е㣬����PO���ӳ�����BC�ڵ�Q��
��ͼ���ھ���ABCD�У�P��AD��һ���㣬OΪBD���е㣬����PO���ӳ�����BC�ڵ�Q���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com