
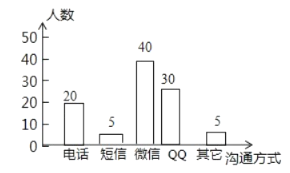
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
【答案】(1)100,108°;(2)补图见解析;(3)600人;(4)![]() .
.
【解析】试题分析:(1)根据喜欢电话沟通的人数与百分比即可求出共抽查人数,求出使用QQ的百分比即可求出QQ的扇形圆心角度数.
(2)计算出短信与微信的人数即可补全统计图.
(3)用样本中喜欢用微信进行沟通的百分比来估计1500名学生中喜欢用微信进行沟通的人数即可求出答案;
(4)列出树状图分别求出所有情况以及甲、乙两名同学恰好选中同一种沟通方式的情况后,利用概念公式即可求出甲、乙两名同学恰好选中同一种沟通方式的概率
试题解析:(1)喜欢用电话沟通的人数为20,所占百分比为20%,∴此次共抽查了:20÷20%=100人,
喜欢用QQ沟通所占比例为: ![]() =
=![]() ,∴QQ”的扇形圆心角的度数为:360°×
,∴QQ”的扇形圆心角的度数为:360°×![]() =108°;
=108°;
(2)喜欢用短信的人数为:100×5%=5人,喜欢用微信的人数为:100﹣20﹣5﹣30﹣5=40.
补充图形,如图所示:
(3)喜欢用微信沟通所占百分比为: ![]() ×100%=40%,
×100%=40%,
∴该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有:1500×40%=600人;
(4)列出树状图,如图所示:
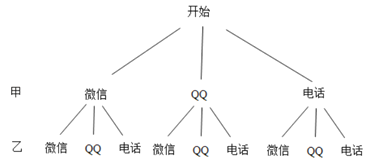
所有情况共有9种情况,其中两人恰好选中同一种沟通方式共有3种情况,甲、乙两名同学恰好选中同一种沟通方式的概率为: ![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,用棋子摆成的“上”字:

第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用 和 枚棋子.
(2)第n个“上”字需用 枚棋子.
(3)如果某一图形共有102枚棋子,你知道它是第几个“上”字吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
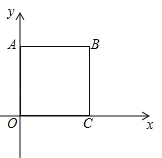
【题目】如图,正方形OABC∽正方形ODEF,它们是以原点O为位似中心的位似图形,位似比为1: ![]() , 点A的坐标为(0,1),则点E的坐标是________或________.
, 点A的坐标为(0,1),则点E的坐标是________或________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
(1)已知点A(2,0),B(0,2![]() ),则以AB为边的“坐标菱形”的最小内角为 ;
),则以AB为边的“坐标菱形”的最小内角为 ;
(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD 表达式;
(3)⊙O的半径为![]() ,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
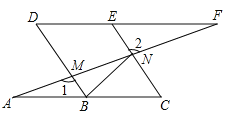
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB,AD为边分别向外侧作等边三角形ABF和等边三角形ADE,连接EB,FD,交点为G.
(1)当四边形ABCD为正方形时,如图①,EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时,如图②,EB和FD具有怎样的数量关系?请加以证明;
(3)如图③,四边形ABCD由正方形到矩形再到一般平行四边形的变化过程中,EB和FD具有怎样的数量关系?请直接写出结论,无需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
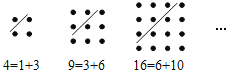
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
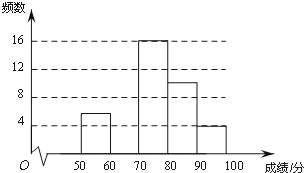
【题目】为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 | a | 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | c | b |
合计 | 50 | 1.00 |
(1)表中的a=______,b=______,c=______;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com