
【题目】已知:如图,点![]() 是
是![]() 的边
的边![]() 上的一点,过点
上的一点,过点![]() 作
作![]() ,
,![]() ,
,![]() ,
,![]() 为垂足,再过点
为垂足,再过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() .
.

(1)求证:![]() ;
;
(2)求证:![]() 垂直平分
垂直平分![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接BD,先根据DE⊥AB,DF⊥BC且DE=DF可知∠ABD=∠DBC,再根据DG∥AB即可得出∠ABD=∠BDG,进而可得出∠BDG=∠DBC,由等角对等边可知DG=BG;
(2)先根据(1)中∠ABD=∠DBC可知∠EDB=∠FDB,由全等三角形的判定定理可得出△BDE≌△BDF,再根据全等三角形的性质可得出BE=BF,DE=DF,故可得出BD垂直平分EF.
证明:(1)连接BD.
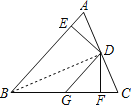
∵DE⊥AB,DF⊥BC且DE=DF,
∴∠ABD=∠DBC,
又∵DG∥AB,
∴∠ABD=∠BDG,
∴∠BDG=∠DBC,
∴DG=BG;
(2)由(1)∠ABD=∠DBC可知,∠EDB=∠FDB,
在△BDE与△BDF中,
∵∠ABD=∠DBC,BD=BD,∠EDB=∠FDB,
∴△BDE≌△BDF,
∴BE=BF,DE=DF,
∴BD垂直平分EF.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,点M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于点F,ME交BC于点G.
(1)写出图中三对相似三角形,并证明其中的一对;
(2)连接FG,如果α=45°,AB=4![]() ,AF=3,求FC和FG的长.
,AF=3,求FC和FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是ABCD的对角线,点E是边AD的中点,连接BE交AC于点F,连接CE,DF,若∠BEC=∠BAC=90°,则sin∠DFE的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元,
(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2014年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理费不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC, D为直线BC上一动点(不与B,C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)当D在线段BC上时,求证:△BAD ≌△CAE;
(2)当点D运动到何处时,AC⊥DE,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com