
| A.正六边形和正方形 | B.正五边形和正八边形 |
| C.正六边形和正三角形 | D.正十边形和正三角形 |


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源:不详 题型:解答题
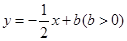 分别交
分别交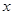 轴,
轴,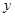 轴于
轴于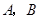 两点,以
两点,以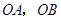 为边作矩形
为边作矩形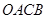 ,
,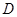 为
为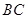 的中点.以
的中点.以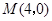 ,
,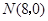 为斜边端点作等腰直角三角形
为斜边端点作等腰直角三角形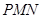 ,点
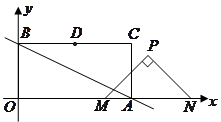
,点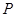 在第一象限,设矩形
在第一象限,设矩形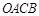 与
与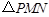 重叠部分的面积为
重叠部分的面积为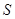 .
.
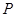 的坐标;
的坐标;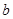 值由小到大变化时,求
值由小到大变化时,求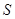 与
与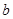 的函数关系式;
的函数关系式;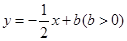 上存在点
上存在点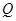 ,使
,使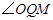 等于
等于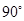 ,请直接写出
,请直接写出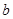 的取值范围
的取值范围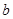 值的变化过程中,若
值的变化过程中,若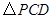 为等腰三角形,且PC=PD,请直接写出
为等腰三角形,且PC=PD,请直接写出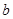 的值.
的值.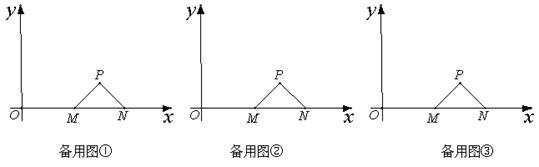
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
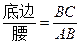 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.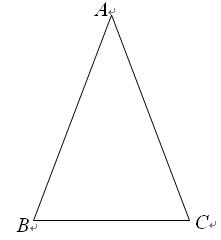
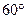 的值为( )
的值为( )A.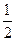 | B.1 | C.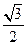 | D.2 |
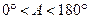 ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .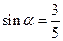 ,其中
,其中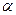 为锐角,试求sad
为锐角,试求sad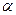 的值.
的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。 时,A、D、M三点构成等腰三角形?并求出点M的坐标。
时,A、D、M三点构成等腰三角形?并求出点M的坐标。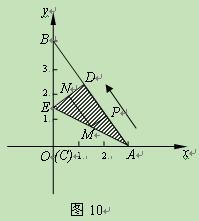
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
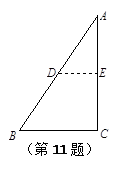 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com