
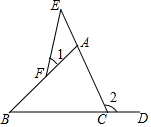
 如图所示,∠1,∠2是不是△ABC的外角?图中还有哪些角可以看作一个三角形的外角?
如图所示,∠1,∠2是不是△ABC的外角?图中还有哪些角可以看作一个三角形的外角? 科目:初中数学 来源: 题型:解答题
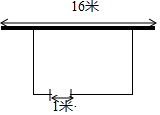 现有32米长的栅栏在长16米的墙边围成面积为130平方米的一个矩形的堆料场.在墙的对面的一边留出1米宽的进出口(如图).这个矩形的长和宽各是多少米?
现有32米长的栅栏在长16米的墙边围成面积为130平方米的一个矩形的堆料场.在墙的对面的一边留出1米宽的进出口(如图).这个矩形的长和宽各是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
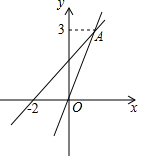 已知正比例函数y=mx与一次函数y=ax+b的图象交于点A(1,3);
已知正比例函数y=mx与一次函数y=ax+b的图象交于点A(1,3);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
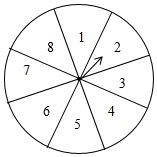 如图,一个均匀的转盘被平均分成8等份,分别标有“1,2,3,4,5,6,7,8”这8个数字,转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:甲、乙两个人参与游戏,甲转动转盘,乙猜数,若猜的数与转盘转出的数相符,则乙获胜;若结果不相符,则甲获胜.(若指针恰好指在分割线上,那么重转一次).
如图,一个均匀的转盘被平均分成8等份,分别标有“1,2,3,4,5,6,7,8”这8个数字,转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:甲、乙两个人参与游戏,甲转动转盘,乙猜数,若猜的数与转盘转出的数相符,则乙获胜;若结果不相符,则甲获胜.(若指针恰好指在分割线上,那么重转一次).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
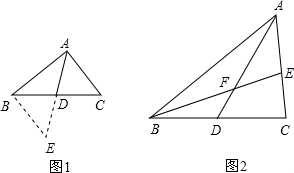 某校数学课外兴趣小组活动时,老师提出如下问题:
某校数学课外兴趣小组活动时,老师提出如下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com