
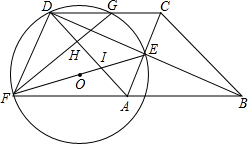
分析 (1)结论:四边形FACD是平行四边形.只要证明AD∥AC,CD∥AF即可.
(2)连接GE,由△EFG∽△CDE,推出$\frac{EF}{CD}$=$\frac{EG}{EC}$,求出EF,即可解决问题.
解答 解:(1)结论:四边形FACD是平行四边形.
理由:∵四边形ABCD是菱形,
∴BD⊥AC,CD∥AB,
∴∠AEB=90°,
∵EF是直径,
∴∠FDE=∠AEB=90°,
∴AD∥AC,∵CD∥AF,
∴四边形FACD是平行四边形.
(2)如图,连接EG.
∵EF是直径,
∴∠EGF=90°,
四边形ABCD是菱形,
∴AC⊥BD,
∴∠EGF=∠DEC=90°,
∵∠EFG=∠EDC,
∴△EFG∽△CDE,
∴$\frac{EF}{CD}$=$\frac{EG}{EC}$,
∵DG=GC,
∴GE=DG=GC=$\frac{1}{2}$CD=$\frac{1}{2}$$\sqrt{{m}^{2}+{n}^{2}}$,
∴$\frac{EF}{\sqrt{{m}^{2}+{n}^{2}}}$=$\frac{\frac{1}{2}\sqrt{{m}^{2}+{n}^{2}}}{m}$,
∴EF=$\frac{{m}^{2}+{n}^{2}}{2m}$,
∴⊙O的面积与菱形ABCD的面积之比=π($\frac{{m}^{2}+{n}^{2}}{4m}$)2÷2mn=$\frac{π({m}^{2}+{n}^{2})}{32{m}^{3}n}$.
点评 本题考查菱形的性质、圆的有关知识、相似三角形的判定和性质、平行四边形顶点等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 张萌在做同步训练时,遇到了下面的一道题,请你帮她做完这道题.
张萌在做同步训练时,遇到了下面的一道题,请你帮她做完这道题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,请你求出乙船的航行方向.
如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,请你求出乙船的航行方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,小明家的观光果园是由两块矩形但重叠了一部分而成的,其重叠部分为正方形,已知果园总面积是116m2,今若将重叠部分改造成休闲区域,求休闲区域的边长.
如图所示,小明家的观光果园是由两块矩形但重叠了一部分而成的,其重叠部分为正方形,已知果园总面积是116m2,今若将重叠部分改造成休闲区域,求休闲区域的边长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com