
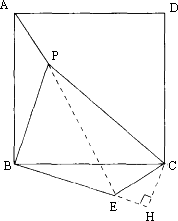
如下图,P是正方形ABCD内-点,已知PA=1,PB=2,PC=3,求正方形ABCD的面积.
|
解:以点B为旋转中心,将△ABP顺时针旋转90°,BA与BC重合,BP=BE,∠PBE=90°,连结PE. ∴△PBE是等腰直角三角形, ∵BP=BE=2, ∴PE=2 ∵EC=PA=1,PC=3, 根据勾股定理逆定理知△PEC为直角三角形,∠PEC=90°. 作CH⊥BE交BE的延长线于H. ∵∠PEB=45°,∠PEC=90°, ∴∠CEH=45°, ∴△CEH为等腰直角三角形,EH=CH= 在Rt△BCH中,根据勾股定理得 BC2=BH2+CH2=(2+ ∴正方形ABCD的面积是5+2 说明:解决有关正方形问题,常将某个图形旋转90°探求解决. 平移变换、轴对称变换、旋转变换都是图形的全等变换,它只改变图形的位置,不改变图形的形状和大小.通过图形的变换,使图形中的线段、角之间建立起新的联系,题目中的隐含条件得以显现,从而有效沟通未知,促进问题的解决. |


科目:初中数学 来源: 题型:
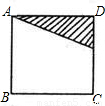
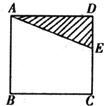 29、如下图,E是正方形ABCD中CD边上任一点,以点A为中心,把△ADE顺时针旋转90°,在给出图形中画出旋转后的图形,并完成下列填空.
29、如下图,E是正方形ABCD中CD边上任一点,以点A为中心,把△ADE顺时针旋转90°,在给出图形中画出旋转后的图形,并完成下列填空.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
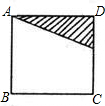 如下图,E是正方形ABCD中CD边上任一点,以点A为中心,把△ADE顺时针旋转90°,在给出图形中画出旋转后的图形,并完成下列填空.
如下图,E是正方形ABCD中CD边上任一点,以点A为中心,把△ADE顺时针旋转90°,在给出图形中画出旋转后的图形,并完成下列填空.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2008-2009学年山东省菏泽市郓城县九年级(上)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com