Question

【题目】公元3世纪初，我国学家赵爽证明勾定理的图形称为“弦图”．1876年美国总统Garfeild用图1（点C、点B、点C′三点共线）进行了勾股定理的证明．△ACB与△BC′B′是一样的直角三角板，两直角边长为a，b，斜边是c．请用此图1证明勾股定理．

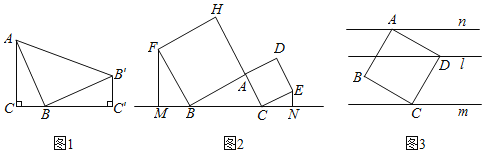
拓展应用l：如图2，以△ABC的边AB和边AC为边长分别向外做正方形ABFH和正方形ACED，过点F、E分别作BC的垂线段FM、EN，则FM、EN、BC的数量关系是怎样？直接写出结论　 　．

拓展应用2：如图3，在两平行线m、n之间有一正方形ABCD，已知点A和点C分别在直线m、n上，过点D作直线l∥n∥m，已知l、n之间距离为1，l、m之间距离为2．则正方形的面积是　 　．

Answer 1

【答案】证明勾股定理：见解析；拓展应用l：FM+EN＝BC；拓展应用2：正方形的面积为5.

【解析】

用a、b、c表示三角形与梯形的面积，再根据梯形的面积等于三个直角三角形的面积和便可得结论；

拓展1．过点A作AP⊥BC于点P，再证明三角形全等便可得结论；

拓展2．过点D作PQ⊥m，分别交m于点P，交n于点Q，然后证明三角形全等，转化线段，再用勾股定理解答.

如图：

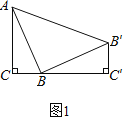
∵点C、点B、点B′三点共线，∠C＝∠C′＝90°，

∴四边形ACC′B′是直角梯形，

∵△ACB与△BC′B′是一样的直角三角板，

∴Rt△ACB≌Rt△BC′B′，

∴∠CAB＝∠C′BB′，AB＝BB′，

∴∠CBA+∠C′BB’＝90°

∴△ABB′是等腰直角三角形，

所以S梯形ACC′B′＝（AC+B′C′）CC′÷2＝，

S△ACB＝，S△BC′B′＝ab，S△ABB′＝c2，

所以，

a2+2ab+b2＝ab+ab+c2，

∴a2+b2＝c2；

拓展1．过A作AP⊥BC于点P，如图2，

则∠BMF＝∠APB＝90°，

∵∠ABF＝90°，

∴∠BFM+∠MBF＝∠MBF+∠ABP，

∴∠BFM＝∠ABP，

在△BMF和△ABP中，

，

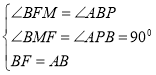∴△BMF≌△ABP（AAS），

∴FM＝BP，

同理，EN＝CP，

∴FM+EN＝BP+CP，

即FM+EN＝BC，

故答案为：FM+EN＝BC；

拓展2．过点D作PQ⊥m，分别交m于点P，交n于点Q，如图3，

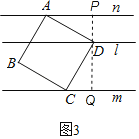
则∠APD＝∠ADC＝∠CQD＝90°，

∴∠ADP+∠DAP＝∠ADP+∠CDQ＝90°，

∴∠DAP＝∠CDQ，

在△APD和△DQC中，

，

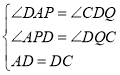∴△APD≌△DQC（AAS），

∴AP＝DQ＝2，

∵PD＝1，

∴AD2＝22+12＝5，

∴正方形的面积为 5，

故答案为：5．