
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
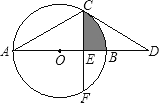
【答案】(1) 30°;(2)![]() -2
-2![]() .
.
【解析】试题分析:(1)连接OC,则△OCD是直角三角形,可求出∠COD的度数;由于∠A与∠COD是同弧所对的圆周角与圆心角.根据圆周角定理即可求得∠A的度数;
(2)由图可知:阴影部分的面积是扇形OCB和Rt△OEC的面积差;那么解决问题的关键是求出半径和OE的长;在Rt△OCE中,∠OCE=∠D=30°,已知了CE的长,通过解直角三角形,即可求出OC、OE的长,由此得解.
试题解析:(1)连接OC,
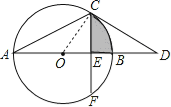
∵CD切⊙O于点C
∴∠OCD=90°
∵∠D=30°
∴∠COD=60°
∵OA=OC
∴∠A=∠ACO=30°;
(2)∵CF⊥直径AB,CF=4![]()
∴CE=2![]()
∴在Rt△OCE中,tan∠COE=![]() ,
,
OE=![]() =2,
=2,
∴OC=2OE=4
∴S扇形BOC=![]() ,S△EOC=
,S△EOC=![]() ×2×2
×2×2![]() =2
=2![]()
∴S阴影=S扇形BOC-S△EOC=![]() -2
-2![]() .
.


科目:初中数学 来源: 题型:
【题目】定义:四条边都相等且四个角都是直角的四边形叫做正方形。我校“快乐走班”数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
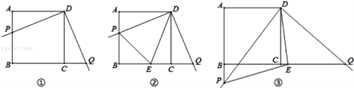
(1)求证:DP=DQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校快乐走班数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°)小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上.
活动一:如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A1A2为第1根小棒.
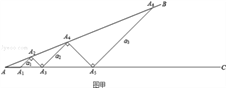
数学思考:
(1)小棒能无限摆下去吗?答: .(填“能“或“不能”)
(2)设AA1=A1A2=A2A3=1.则θ= 度;
活动二:如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
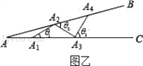
数学思考:
(3)若只能摆放5根小棒,求θ的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com