【题目】重庆市居民用水的水价实行阶梯收费，标准如下表：
每户居民每月用水量 | 水费单价（元） |
|
|
|
|
| 4.5 |
（1）已知张三家5月份用水13吨，缴费47元，6月份用水15吨，缴费55元．请根据上述信息，求
、
的值．
（2）在（1）的条件下，由于天气变热，7月份是用水高峰期，张三家计划7月份水费支出不超过100元，那么张三家7月份最多可用多少吨水？
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．
（1）求证：四边形ADEF是平行四边形；
（2）求证：∠DHF=∠DEF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点A(t+1,t+2),点B(t+3,t+1),将点A向右平移3个长度单位，再向下平移4个长度单位得到点C.
（1）用t表示点C的坐标为_______;用t表示点B到y轴的距离为___________;
（2）若t=1时，平移线段AB，使点A、B到坐标轴上的点
、
处，指出平移的方向和距离，并求出点、的坐标；
（3）若t=0时，平移线段AB至MN（点A与点M对应），使点Ｍ落在ｘ轴的负半轴上，三角形MNB的面积为4，试求点M、N的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校．以下是他本次上学所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：
（1）小明家到学校的路程是 米．
（2）小明在书店停留了 分钟．
（3）本次上学途中，小明一共行驶了 米．一共用了 分钟．
（4）我们认为骑单车的速度超过 300 米/分就超过了安全限度．问：在整个上学途中哪个时间段小明的骑车速度最快，最快速度为多少，在安全限度内吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直角坐标系中，
的顶点都在网格点上，其中，
点坐标为
，
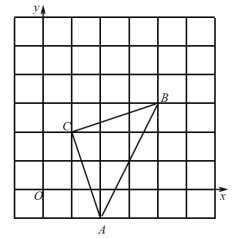
（1）写出点
、
的坐标：（____，____）、（____，____）
（2）将先向左平移
个单位长度，再向上平移
个单位长度，得到
，画出；
（3）写出三个顶点坐标
（___，___）、
（___，___）、
（___，___）；
（4）求的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了提高产品的附加值，某公司计划将研发生产的1200件新产品进行精加工后再投放市场．现有甲、乙两个工厂都具备加工能力，公司派出相关人员分别到这两个工厂了解情况，获得如下信息：
信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；
信息二：乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍．
根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知
，
是等边三角形，点
为射线
上任意一点（点与点
不重合），连结
，将线段绕点
逆时针旋转
得到线段
，连结
并延长交射线于点
．
（1）如图1，当
时，
________
，猜想
________；
（2）如图2，当点为射线上任意一点时，猜想
的度数，并说明理由；
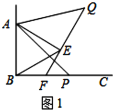
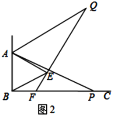
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠BAC=90°，D、E分别是AB、BC的中点，F在CA延长线上，∠FDA=∠B，AC=6，AB=8，则四边形AEDF的周长为（ ）
A. 16 B. 20 C. 18 D. 22
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）阅读思考：
小迪在学习过程中，发现“数轴上两点间的距离”可以用“表示这两点数的差”来表示，探索过程如下：
如图1所示，线段AB，BC，CD的长度可表示为：AB＝3＝4﹣1，BC＝5＝4﹣（﹣1），CD＝3＝（﹣1）﹣（﹣4），于是他归纳出这样的结论：如果点A表示的数为a，点B表示的数为b，当b＞a时，AB＝b﹣a（较大数﹣较小数）．
（2）尝试应用：
①如图2所示，计算：OE＝ ，EF＝ ；
②把一条数轴在数m处对折，使表示﹣19和2019两数的点恰好互相重合，则m＝ ；
（3）问题解决：
①如图3所示，点P表示数x，点M表示数﹣2，点N表示数2x+8，且MN＝4PM，求出点P和点N分别表示的数；
②在上述①的条件下，是否存在点Q，使PQ+QN＝3QM？若存在，请直接写出点Q所表示的数；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
