Question

17．在平面直角坐标系中，△ABC的顶点坐标分别为A（2，0），B（0，4），C（-3，2）．
（1）如图1，求△ABC的面积．
（2）若点P的坐标为（m，0），
①请直接写出线段AP的长为|m-2|（用含m的式子表示）；
②当S_△PAB=2S_△ABC时，求m的值．
（3）如图2，若AC交y轴于点D，直接写出点D的坐标为（0，$\frac{4}{5}$）．

Answer 1

分析 （1）过点C作CD⊥x轴，垂足为D，过点B作BE⊥CD，交DC延长线于E，过点A作AF⊥BE，交EB延长线于F，由题意得出∴D（-3，0），E（-3，4），F（2，4）．得出AD=5，CD=2，BE=3，CE=2，DE=4，BF=2，AF=4．S_△ABC=S_矩形ADEF-S_△ACD-S_△BCE-S_△ABF，即可得出结果；
（2）①根据题意容易得出结果；
②由三角形面积关系得出方程，解方程即可；
（3）与待定系数法求出直线AC的解析式，即可得出点D的坐标．

解答 解：（1）过点C作CD⊥x轴，垂足为D，过点B作BE⊥CD，交DC延长线于E，
过点A作AF⊥BE，交EB延长线于F．如图所示：
∵A（2，0），B（0，4），C（-3，2）
∴D（-3，0），E（-3，4），F（2，4）．
∴AD=5，CD=2，BE=3，CE=2，DE=4，BF=2，AF=4．
∴S_△ABC=S_矩形ADEF-S_△ACD-S_△BCE-S_△ABF=$AD•DE-\frac{1}{2}AD•CD-\frac{1}{2}CE•BE-\frac{1}{2}BF•AF$=$5×4-\frac{1}{2}×5×2-\frac{1}{2}×2×3-\frac{1}{2}×2×4$=8．
答：△ABC的面积是8．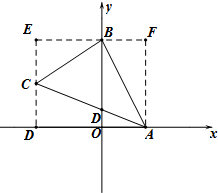
（2）①根据题意得：AP=|m-2|；
故答案为：|m-2|；
②∵S_△PAB=2S_△ABC
∴$\frac{1}{2}•AP•BO=2×8$
∴AP=|m-2|=8，
∴m-2=8或m-2=-8，
∴m=10或m=-6；
（3）设直线AC的解析式为y=kx+b，
根据题意得：$\left\{\begin{array}{l}{2k+b=0}\\{-3k+b=2}\end{array}\right.$，
解得：k=-$\frac{2}{5}$，b=$\frac{4}{5}$；
∴直线AC的解析式为y=-$\frac{2}{5}$x+$\frac{4}{5}$，
当x=0时，y=$\frac{4}{5}$，
∴D（0，$\frac{4}{5}$），；
故答案为：（0，$\frac{4}{5}$）．

点评 本题考查了坐标与图形性质、三角形面积的计算方法、待定系数法求直线的解析式；熟练掌握坐标与图形性质，求出直线AC的解析式是解决问题（3）的关键．