
【题目】已知每件![]() 奖品价格相同,每件
奖品价格相同,每件![]() 奖品价格相同,老师要网购
奖品价格相同,老师要网购![]() 两种奖品
两种奖品![]() 件,若购买
件,若购买![]() 奖品
奖品![]() 件、
件、![]() 奖品
奖品![]() 件,则微信钱包内的钱会差
件,则微信钱包内的钱会差![]() 元;若购买
元;若购买![]() 奖品
奖品![]() 件、
件、![]() 奖品
奖品![]() 件,则微信钱包的钱会剩余
件,则微信钱包的钱会剩余![]() 元,老师实际购买了
元,老师实际购买了![]() 奖品
奖品![]() 件,
件,![]() 奖品
奖品![]() 件,则微信钱包内的钱会剩余__________元.
件,则微信钱包内的钱会剩余__________元.
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,对于任意两点![]() ,
,![]() ,若点
,若点![]() 满足
满足![]() ,
,![]() ,那么称点
,那么称点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
例如:![]() ,
,![]() ,当点
,当点![]() 满是
满是![]() ,
,![]() 时,则点
时,则点![]() 是点
是点![]() ,
,![]() 的融合点,
的融合点,

(1)已知点![]() ,
,![]() ,
,![]() ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.
(2)如图,点![]() ,点
,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
①试确定![]() 与
与![]() 的关系式.
的关系式.
②若直线![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
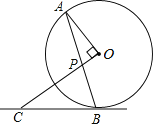
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某织布厂有150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30m,或利用所织布制衣4件,制衣一件需要布1.5m,将布直接出售,每米布可获利2元,将布制成衣后出售,每件可获利25元,若每名工人每天只能做一项工作,且不计其他因素,设安排x名工人制衣.
(1)一天中制衣所获利润P是多少(用含x的式子表示);
(2)一天中剩余布所获利润Q是多少 (用含x的式子表示);.
(3)一天当中安排多少名工人制衣时,所获利润为11806元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得a= ,b= ;
)2,用含m、n的式子分别表示a、b,得a= ,b= ;
(2)试着把7+4![]() 化成一个完全平方式.
化成一个完全平方式.
(3)若a是216的立方根,b是16的平方根,试计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 分别在
分别在![]() 的边
的边![]() 上运动(不与点
上运动(不与点![]() 重合),
重合),![]() 是
是![]() 的平分线,
的平分线,![]() 的延长线交角
的延长线交角![]() 的平分线于点
的平分线于点![]() .
.

(1)若![]() ,求
,求![]() 的度数.
的度数.
(2)若![]() ,求
,求![]() 的度数.
的度数.
(3)若![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,
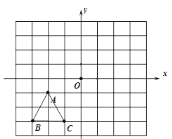
(1)若将△ABC 向右平移三个单位长度得到△A1B1C1,则点 A1 的坐标为________![]()
(2)若△ABC 与△A2B2C2 关于原点 O 成中心对称,则点 A2 的坐标________;
(3)画出△ABC 绕原点 O 顺时针旋转 90°后的对应图形△A3B3C3,并写出 A3 的坐标_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米![]() 小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点,过了5秒后,测得小汽车所在的B点与车速检测仪A之间的距离为100米.
小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点,过了5秒后,测得小汽车所在的B点与车速检测仪A之间的距离为100米.
![]() 求BC间的距离;
求BC间的距离;![]() 这辆小汽车超速了吗?请说明理由.
这辆小汽车超速了吗?请说明理由.

【答案】这辆小汽车没有超速.
【解析】
(1)根据勾股定理求出BC的长;
(2)直接求出小汽车的时速,进行比较得出答案.
(1)在Rt△ABC中,AC=60 m,
AB=100 m,且AB为斜边,根据勾股定理,得BC=80 m.
(2)这辆小汽车没有超速.
理由:∵80÷5=16(m/s),
而16 m/s=57.6 km/h,57.6<70,
∴这辆小汽车没有超速.
【点睛】
考查勾股定理的应用,熟练掌握勾股定理是解题的关键.
【题型】解答题
【结束】
19
【题目】已知:如图,线段AC和BD相交于点G,连接AB,CD,E是CD上一点,F是DG上一点,![]() ,且
,且![]() .
.
![]() 求证:
求证:![]() ;
;![]() 若
若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com