
分析 (1)设降价x元时,每星期盈利为6125元,根据:每件利润×销售量=总利润,列方程求解可得;
(2)根据:利润=单件利润×售出的总件数列出函数表达式,根据x=-$\frac{b}{2a}$时,y有最大值.
解答 解:(1)设降价x元时,每星期盈利为6125元,
根据题意,得:(20-x)(300+20x)=6125,
解得:x=2.5,
答:降价2.5元时,每星期盈利为6125元.
(2)设降价x元时,每星期的盈利为y元,
则y=(60-x)(300+20x)-40(300+20x)=-20x2+100x+6000.
因为降价要确保盈利,所以40<60-x≤60,
解得:0≤x<20,
∴当x=$\frac{100}{2×(-20)}$=2.5时,y有最大值$\frac{4×(-20)×6000-10{0}^{2}}{4×(-20)}$=6125,
答:当降价2.5元时,利润最大且为6125元.
点评 本题主要考查了二次函数的应用,根据题意正确列出代数式和函数表达式是解决问题的关键.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:填空题
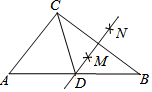 如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D;连结CD.若AB=8,AC=3,则△ACD的周长为11.
如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D;连结CD.若AB=8,AC=3,则△ACD的周长为11.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
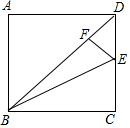 如图,正方形ABCD的边长为5,连接BD,在线段CD上取一点E,在线段BD上取点F,使得∠BEC=∠DEF,当S△DEF=$\frac{1}{3}$S△EFB时,在线段BC上有一点G,使FG+EG最短,则CG=$\frac{5}{9}$.
如图,正方形ABCD的边长为5,连接BD,在线段CD上取一点E,在线段BD上取点F,使得∠BEC=∠DEF,当S△DEF=$\frac{1}{3}$S△EFB时,在线段BC上有一点G,使FG+EG最短,则CG=$\frac{5}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com