
已知:如图,四边形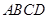 是平行四边形,
是平行四边形,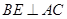 于
于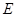 ,
,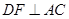 于
于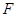 .求证:
.求证: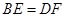 .
.
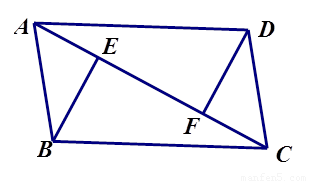
【解析】证线段所在的三角形全等.根据“AAS”可证△ABE≌△CDF或△ADF≌△CBE.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
已知:如图①,四边形![]() 是正方形,
是正方形,![]() 是等边三角形,
是等边三角形,![]() 为对角线
为对角线![]() (不含
(不含![]() 点)上任意一点,将
点)上任意一点,将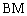 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() 、
、![]() 、
、![]() 。
。
1.求证:![]()
2.①当![]() 点在何处时,
点在何处时,![]() 的值最小;
的值最小;
②当![]() 点在何处时,
点在何处时,![]() 的值最小,并说明理由;
的值最小,并说明理由;
3.当![]() 的最小值为
的最小值为![]() 时,求正方形的边长。
时,求正方形的边长。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年天津市河西区九年级上学期期中质量调查数学卷 题型:解答题
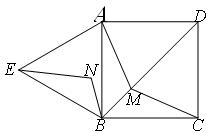
已知:如图①,四边形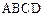 是正方形,
是正方形,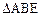 是等边三角形,
是等边三角形, 为对角线
为对角线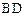 (不含
(不含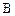 点)上任意一点,将
点)上任意一点,将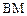 绕点
绕点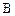 逆时针旋转
逆时针旋转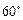 得到
得到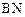 ,连接
,连接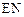 、
、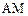 、
、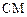 。
。
(I)求证: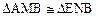
(II)①当 点在何处时,
点在何处时,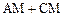 的值最小;
的值最小;
②当 点在何处时,
点在何处时,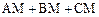 的值最小,并说明理由;
的值最小,并说明理由;
(III)当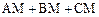 的最小值为
的最小值为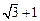 时,求正方形的边长。
时,求正方形的边长。
查看答案和解析>>
科目:初中数学 来源:2012届天津市河西区九年级上学期期中质量调查数学卷 题型:解答题
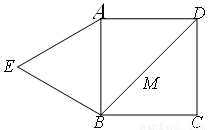
已知:如图①,四边形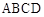 是正方形,
是正方形,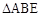 是等边三角形,
是等边三角形, 为对角线
为对角线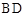 (不含
(不含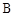 点)上任意一点,将
点)上任意一点,将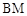 绕点
绕点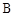 逆时针旋转
逆时针旋转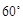 得到
得到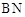 ,连接
,连接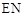 、
、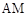 、
、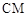 。
。

(I)求证:
(II)①当 点在何处时,
点在何处时,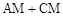 的值最小;
的值最小;
②当 点在何处时,
点在何处时,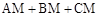 的值最小,并说明理由;
的值最小,并说明理由;
(III)当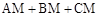 的最小值为
的最小值为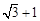 时,求正方形的边长。
时,求正方形的边长。
查看答案和解析>>
科目:初中数学 来源:2010--2011学年山东肥城马埠中学毕业班月考模数学试卷 题型:解答题
已知:如图,四边形 是矩形,
是矩形,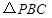 和
和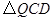 都是等边三角形,且点
都是等边三角形,且点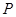 在矩形上方,点
在矩形上方,点 在矩形内.
在矩形内.
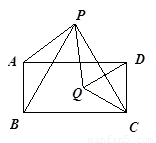
1.求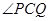 的度数
的度数
2.求证: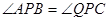
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com