
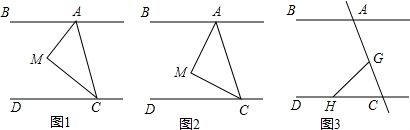
分析 (1)根据角平分线的性质和三角形内角和定理即可得出答案;
(2)过M作MF∥AB,根据平行线的性质得出∠BAM=∠AMF,∠FMC=∠DCM,再根据∠M=90°,即可得出∠BAM+∠MCD=90°;
(3)过点G作GP∥AB,根据平行线的性质得出∠BAC=∠PGC,∠CHG=∠PGH,从而得出∠BAC=∠CHG+∠CGH.
解答 解:(1)∵CM平分∠ACD,AM平分∠BAC,
∴∠BAC=2∠MAC,∠ACD=2∠ACM,
∵∠MAC+∠ACM=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAM+∠MCD=90°;
理由:如图2,过M作MF∥AB,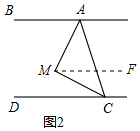
∵AB∥CD,
∴MF∥AB∥CD,
∴∠BAM=∠AMF,∠FMC=∠DCM,
∵∠M=90°,
∴∠BAM+∠MCD=90°;
(3)过点G作GP∥AB,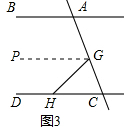
∵AB∥CD
∴GP∥CD,
∴∠BAC=∠PGC,∠CHG=∠PGH,
∴∠PGC=∠CHG+∠CGH,
∴∠BAC=∠CHG+∠CGH.
点评 此题考查了平行线的判定与性质,用到的知识点是三角形内角和定理以及平行线的判定与性质,关键是根据题意做出辅助线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com