
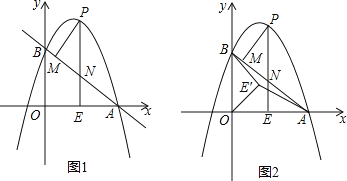
【题目】如图1,抛物线![]() 与
与![]() 轴交于点A(4,0),与
轴交于点A(4,0),与![]() 轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作
轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作![]() 轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求![]() 的值和直线AB的函数表达式;
的值和直线AB的函数表达式;
(2)在P点运动的过程中,请用含m的代数式表示线段PN;
(3)设△PMN的周长为![]() ,△AEN的周长为
,△AEN的周长为![]() ,若
,若![]() ,求m的值;
,求m的值;
(4)如图2,在(3)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;直线AB解析式为y=
;直线AB解析式为y=![]() ;(2)PN=
;(2)PN=![]() m2+3m ;(3)2;(4)
m2+3m ;(3)2;(4)![]()
【解析】试题解析:(1)(1)令y=0,求出抛物线与x轴交点,列出方程即可求出a,根据待定系数法可以确定直线AB解析式;(2)由△PNM∽△ANE,推出![]() ,列出方程即可解决问题;(3)在y轴上 取一点M使得OM′=
,列出方程即可解决问题;(3)在y轴上 取一点M使得OM′=![]() ,构造相似三角形,可以证明AM′就是
,构造相似三角形,可以证明AM′就是![]() 的最小值;
的最小值;
试题分析:
(1)∵抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),
∴a=﹣![]() . ……………………………………………2分
. ……………………………………………2分
∵A(4,0),B(0,3),
设直线AB解析式为y=kx+b,则![]() ,
,
解得![]() ,
,
∴直线AB解析式为y=﹣![]() x+3 ……………………………………………4分
x+3 ……………………………………………4分
设点P(m,﹣![]() m2+
m2+![]() m+3)
m+3)
点N在直线AB上则N(![]() )
)
∴PN=﹣![]() m2+
m2+![]() m+3﹣(﹣
m+3﹣(﹣![]() m+3)=﹣
m+3)=﹣![]() m2+3m ………………………………6分
m2+3m ………………………………6分
(3)如图1中,
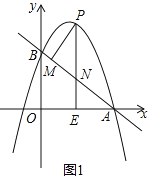
∵PM⊥AB,PE⊥OA,
∴∠PMN=∠AEN,∵∠PNM=∠ANE,
∴△PNM∽△ANE, ……………………………………………8分
∴![]() =
=![]() ,
,
∵NE∥OB,
∴![]() =
=![]() ,
,
∴AN=![]() (4﹣m),
(4﹣m),
∵PN=﹣![]() m2+
m2+![]() m+3﹣(﹣
m+3﹣(﹣![]() m+3)=﹣
m+3)=﹣![]() m2+3m,
m2+3m,
∴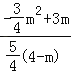 =
=![]() ,
,
解得m=2 ……………………………………………10分
(3)如图2中,在y轴上 取一点M′使得OM′=![]() ,连接AM′交PE于E′,
,连接AM′交PE于E′,
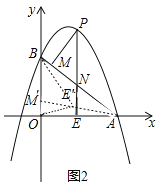
∵OE′=2,OM′OB=![]() ×3=4,
×3=4,
∴OE′2=OM′OB,
∴![]() =
=![]() ,∵∠BOE′=∠M′OE′,
,∵∠BOE′=∠M′OE′,
∴△M′OE′∽△E′OB,
∴![]() =
=![]() =
=![]() ,
,
∴M′E′=![]() BE′,
BE′,
∴AE′+![]() BE′=AE′+E′M′=AM′,此时AE′+
BE′=AE′+E′M′=AM′,此时AE′+![]() BE′最小(两点间线段最短,A、M′、E′共线时),
BE′最小(两点间线段最短,A、M′、E′共线时),
最小值=AM′=![]() =
=![]()
![]() 。
。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( ) 
A.4
B.8
C.16
D.无法计算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b均为正整数,则数据a、b、10、11、11、12的众数和中位数可能分别是( )
A. 10、10B. 11、11C. 10、11.5D. 12、10.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列整式乘法的运算中,正确的是( )
A. (a+b)(a﹣b)=a2﹣b2 B. (a+b)2=a2+b2
C. (a+b)(a﹣b)=2a D. (a﹣b)2=a2﹣2ab﹣b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下述命题中,真命题有( )
(1)对角线互相垂直的四边形是菱形
(2)三个角的度数之比为1:3:4的三角形是直角三角形
(3)对角互补的平行四边形是矩形
(4)三边之比为1: ![]() :2的三角形是直角三角形.
:2的三角形是直角三角形.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线y=(x+1)2+3有以下结论:①抛物线开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>1时,y随x的增大而减小.其中正确结论的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com