练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．把（x-a）3-（a-x）2分解因式的结果为（　　）
    A．（x-a）2（x-a+1）B．（x-a）2（x-a-1）C．（x-a）2（x+a）D．（a-x）2（x-a-1）

    分析 原式变形后，提取公因式即可得到结果．

    解答 解：原式=（x-a）3-（x-a）2=（x-a）2（x-a-1），
    故选B

    点评 此题考查了因式分解-提公因式法，熟练掌握提取公因式的方法是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．如图，四边形ABCD中，BC∥AD，BC=AB，∠BAD=90°，∠D=45°，E是BC上一点，F是CD上一点，
    （1）若EF⊥AE，求证：AE=EF．
    （2）若AE=EF，求证：EF⊥AE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，在等边△ABC中，P是BC下方一动点，且∠BPC=120°，PB、PC是关于x的方程（a-1）x2-9（a-1）x+b=c的两实数根，求PA的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

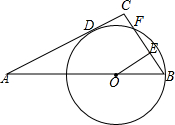    6．如图，Rt△ABC，∠C=90°，BC=3，点O在AB上，OB=2，以OB长为半径的⊙O与AC相切于点D，交BC于点F，OE⊥BC于点E，则弦BF的长为2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．已知梯形的面积是6，高是4，则梯形的上底y关于下底x的函数关系式是y=-x+3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．为备战2016年里约奥运会，中国女排的姑娘们刻苦训练，为国争光，如图，已知排球场的长度OD为18米，位于球场中线处球网的高度AB为2.43米，一队员站在点O处发球，排球从点O的正上方1.8米的C点向正前方飞出，当排球运行至离点O的水平距离OE为7米时，到达最高点G建立如图所示的平面直角坐标系．
    （1）当球上升的最大高度为3.2米时，求排球飞行的高度y（单位：米）与水平距离x（单位：米）的函数关系式．（不要求写自变量x的取值范围）．
    （2）在（1）的条件下，对方距球网0.5米的点F处有一队员，他起跳后的最大高度为3.1米，问这次她是否可以拦网成功？请通过计算说明．
    （3）若队员发球既要过球网，又不出边界，问排球飞行的最大高度h的取值范围是多少？（排球压线属于没出界）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

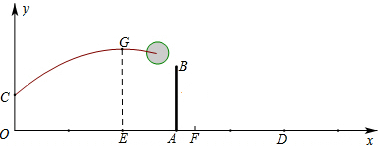
    10．如图，在长方形ABCD中，AD=10，AB=4，点O是BC中点，点P在AD边上运动，当△OCP是等腰三角形时，试求出所有AP可能的长．（备注：若答案不唯一，则每一种情形需有详细的解答过程．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

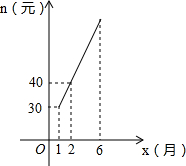    7．某商店今年1-6月份经营A、B两种电子产品，已知A产品每个月的销售数量y（件）与月份x（1≤x≤6且x为整数）之间的关系如表：
    x123456
    y600300200150120100
    A产品每个月的售价z（元）与月份x之间的函数关系式为：z=10x；已知B产品每个月的销售数量m（件）与月份x之间的关系为：m=-2x+62，B产品每个月的售价n（元）与月份x之间存在如图所示的变化趋势；
    （1）请观察题中表格，用所学过的一次函数或反比例函数的有关知识，直接写出y与x的函数关系式；
    （2）请观察如图所示的变化趋势，求出n与x的函数关系式；
    （3）求出商店1-6月份经营A、B两种电子产品的销售总额w与月份x之间的函数关系式；
    （4）今年7月份，商店调整了A、B两种电子产品的价格，A产品价格在6月份基础上增加a%，B产品价格在6月份基础上减少a%，结果7月份A产品的销售数量比6月份减少2a%，B产品的销售数量比6月份增加2a%．若调整价格后7月份的销售总额比6月份的销售总额少2000元，请根据以下参考数据估算a的值．
    （参考数据：6.32=39.69，6.42=40.91，6.52=42.25，6.62=43.56）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知直线y=kx-8k（k＜0）与x轴、y轴分别交于A点、B点，抛物线
    y=ax2+x+c经过A点和B点，其顶点为M．
    （1）直线y=kx-8k总经过一个固定的点，请直接写出这个固定点的坐标：（8，0）；
    （2）当抛物线的对称轴位于直线x=2的右侧时，求k的取值范围；
    （3）当k=-$\frac{3}{4}$时，请判断∠AMB是钝角、直角、锐角中的哪一种，并说明理由．

    查看答案和解析>>

    同步练习册答案