
【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN=![]() ;③BP=4PK;④PMPA=3PD2,其中正确的是( )
;③BP=4PK;④PMPA=3PD2,其中正确的是( )
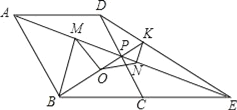
A.①②③B.①②④C.①③④D.②③④
【答案】B
【解析】
根据菱形的性质得到AD∥BC,根据平行线的性质得到对应角相等,根据全等三角形的判定定理△ADP≌△ECP,由相似三角形的性质得到AD=CE,作PI∥CE交DE于I,根据点P是CD的中点证明CE=2PI,BE=4PI,根据相似三角形的性质得到![]() ,得到BP=3PK,故③错误;作OG⊥AE于G,根据平行线等分线段定理得到MG=NG,又OG⊥MN,证明△MON是等腰三角形,故①正确;根据直角三角形的性质和锐角三角函数求出∠OMN=
,得到BP=3PK,故③错误;作OG⊥AE于G,根据平行线等分线段定理得到MG=NG,又OG⊥MN,证明△MON是等腰三角形,故①正确;根据直角三角形的性质和锐角三角函数求出∠OMN=![]() ,故②正确;然后根据射影定理和三角函数即可得到PMPA=3PD2,故④正确.
,故②正确;然后根据射影定理和三角函数即可得到PMPA=3PD2,故④正确.
解:作PI∥CE交DE于I,
∵四边形ABCD为菱形,
∴AD∥BC,
∴∠DAP=∠CEP,∠ADP=∠ECP,
在△ADP和△ECP中,
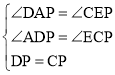 ,
,
∴△ADP≌△ECP,
∴AD=CE,
则![]() ,又点P是CD的中点,
,又点P是CD的中点,
∴![]() ,
,
∵AD=CE,
∴![]() ,
,
∴BP=3PK,
故③错误;
作OG⊥AE于G,
∵BM丄AE于M,KN丄AE于N,
∴BM∥OG∥KN,
∵点O是线段BK的中点,
∴MG=NG,又OG⊥MN,
∴OM=ON,
即△MON是等腰三角形,故①正确;
由题意得,△BPC,△AMB,△ABP为直角三角形,
设BC=2,则CP=1,由勾股定理得,BP=![]() ,
,
则AP=![]() ,
,
根据三角形面积公式,BM=![]() ,
,
∵点O是线段BK的中点,
∴PB=3PO,
∴OG=![]() BM=
BM=![]() ,
,
MG=![]() MP=
MP=![]() ,
,
tan∠OMN=![]() ,故②正确;
,故②正确;
∵∠ABP=90°,BM⊥AP,
∴PB2=PMPA,
∵∠BCD=60°,
∴∠ABC=120°,
∴∠PBC=30°,
∴∠BPC=90°,
∴PB=![]() PC,
PC,
∵PD=PC,
∴PB2=3PD,
∴PMPA=3PD2,故④正确.
故选B.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】如图所示的![]() 正方形网格中,每个小正方形的边长均为1个单位,
正方形网格中,每个小正方形的边长均为1个单位,![]() 均在格点上,按如下要求作图.
均在格点上,按如下要求作图.
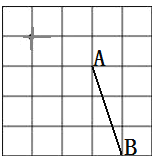
(1)将线段![]() 绕
绕![]() 点按顺时针方向旋转90°,
点按顺时针方向旋转90°,![]() 点对应点为
点对应点为![]() 点;
点;
(2)以![]() 为对角线画一个各边都不相等的四边形
为对角线画一个各边都不相等的四边形![]() ,且
,且![]() ,此时四边形
,此时四边形![]() 的面积为_______.
的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,点P、Q分别在BC、CD上,∠PAQ=∠B.
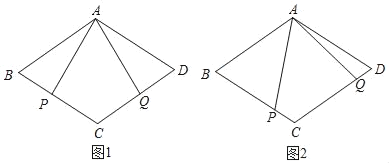
(1)如图1,若AP⊥BC,求证:AP=AQ;
(2)如图2,若点P为BC上一点,AP=AQ仍成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共“金山银山,不如绿水青山”.某市不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:
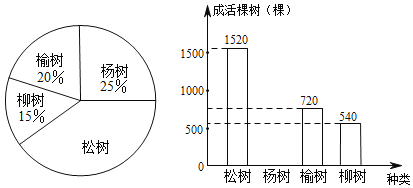
(1)扇形统计图中松树所对的圆心角为 度,并补全条形统计图.
(2)该市今年共种树16万棵,成活了约多少棵?
(3)园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平行四边形ABCD中,M是BC边的中点,E是边BA延长线上的一点,连结EM,分别交线段AD、AC于点F、G.
(1)求证:![]() ;
;
(2)当BC2=2BABE时,求证:∠EMB=∠ACD.
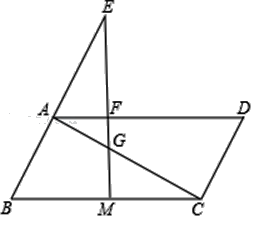
查看答案和解析>>
科目:初中数学 来源: 题型:
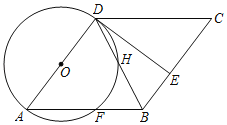
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
(1)求证:△DAF≌△DCE.
(2)求证:DE是⊙O的切线.
(3)若BF=2,DH=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com