
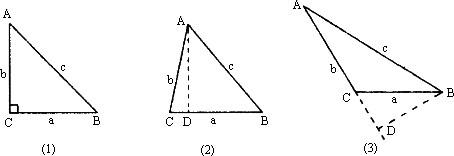
在△ABC中,BC=a,AC=b,AB=c若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
|
解:若△ABC为锐角三角形,有a2+b2>c2. 若△ABC为钝角三角形,(且∠C为钝角),有a2+b2<c2. (1)△ABC为锐角三角形,作AD⊥BC于D. 设CD=x,BD=a-x. 由勾股定理,b2-x2=c2-(a-x)2, 即b2-x2=c2-a2+2ax-x2, ∴a2+b2=c2+2ax>x2即a2+b2>c2. (2)△ABC为钝角三角形,作BD⊥AC交AC延长线于D. 设CD=x,则BD2=a2-x2. 由勾股定理,得(b+x)2+a2-x2=c2, 即a2+b2+2bx=c2, ∴a2+b2<x2. 分析:通过作一边上的高将三角形转化为直角三角形,再利用勾股定理进而求得. |


科目:初中数学 来源: 题型:
 AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于 ( )
AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于 ( )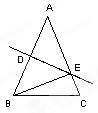
| A.12cm | B.10cm | C.8cm | D.6cm |
查看答案和解析>>
科目:初中数学 来源:2012届福建厦门外国语学校九年级中考模拟数学试卷(带解析) 题型:解答题
已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
【小题1】判断DE与⊙O的位置关系,并证明你的结论
【小题2】若DE的长为2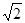 ,cosB=,求⊙O的半径.
,cosB=,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建厦门外国语学校九年级中考模拟数学试卷(解析版) 题型:解答题
已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
1.判断DE与⊙O的位置关系,并证明你的结论
2.若DE的长为2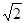 ,cosB=,求⊙O的半径.
,cosB=,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省八年级12月月考数学卷 题型:选择题
如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于 ( )

A.12cm B.10cm C. 8cm D. 6cm
查看答案和解析>>
科目:初中数学 来源:2010-2011学年福建省泉州市洛江区初三上学期期末数学卷 题型:选择题
如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于 ( )
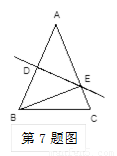
A.12cm B.10cm C. 8cm D. 6cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com