
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬OĪŖ×ų±źŌµć£¬Ö±Ļßy=©x©3ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻßy=x2+bx+c¾¹żA”¢CĮ½µć£¬ÓėxÖį½»ÓŚĮķŅ»µćB
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
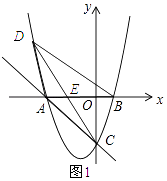
£Ø2£©µćDŹĒµŚ¶žĻóĻŽÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓAD”¢BD”¢CD£¬µ±S”÷ACD= ![]() SĖıߊĪACBDŹ±£¬ĒóDµć×ų±ź£»
SĖıߊĪACBDŹ±£¬ĒóDµć×ų±ź£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Į¬½ÓBC£¬¹żµćD×÷DE”ĶBC£¬½»CBµÄŃÓ³¤ĻßÓŚµćE£¬µćPŹĒµŚČżĻóĻŽÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬µćP¹ŲÓŚµćBµÄ¶Ō³ĘµćĪŖµćQ£¬Į¬½ÓQE£¬ŃÓ³¤QEÓėÅ×ĪļĻßŌŚA”¢DÖ®¼äµÄ²æ·Ö½»ÓŚŅ»µćF£¬µ±”ĻDEF+”ĻBPC=”ĻDBEŹ±£¬ĒóEFµÄ³¤£®
”¾“š°ø”æ
£Ø1£©
½ā£ŗ”ßĮīx=0µĆ£ŗy=©3£¬
”ąC£Ø0£¬©3£©£®
Įīy=0µĆ£ŗ©x©3=0£¬½āµĆx=©3£¬
”ąA£Ø©3£¬0£©£®
½«A”¢CĮ½µćµÄ×ų±ź“śČėÅ×ĪļĻߵĽāĪöŹ½µÄ£ŗ ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ ![]() £®
£®
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=x2+2x©3
£Ø2£©
½ā£ŗČēĶ¼1ĖłŹ¾£ŗ
Įīy=0µĆ£ŗx2+2x©3=0£¬½āµĆx=©3»ņx=1£®
”ąAB=4£®
”ßS”÷ACD= ![]() SĖıߊĪACBD£¬
SĖıߊĪACBD£¬
”ąS”÷ADC£ŗS”÷DCB=3£ŗ5£®
”ąAE£ŗEB=3£ŗ5£®
”ąAE=4”Į ![]() =
= ![]() £®
£®
”ąµćEµÄ×ų±źĪŖ£Ø© ![]() £¬0£©£®
£¬0£©£®
ÉčECµÄ½āĪöŹ½ĪŖy=kx+b£¬½«µćCŗĶµćEµÄ×ų±ź“śČėµĆ£ŗ 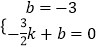 £¬
£¬
½āµĆ£ŗk=©2£¬b=©3£®
”ąÖ±ĻßCEµÄ½āĪöŹ½ĪŖy=©2x©3£®
½«y=©2x©3Óėy=x2+2x©3ĮŖĮ¢£¬½āµĆ£ŗx=©4»ņx=0£ØÉįČ„£©£¬
½«x=©4“śČėy=©2x©3µĆ£ŗy=5£®
”ąµćDµÄ×ų±źĪŖ£Ø©4£¬5£©
£Ø3£©
½ā£ŗČēĶ¼2ĖłŹ¾£ŗ¹żµćD×÷DN”ĶxÖį£¬“¹×ćĪŖN£¬¹żµćP×÷PM”ĶxÖį£¬“¹×ćĪŖM£®
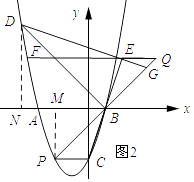
ÉčÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=kx+b£¬½«µćCŗĶµćBµÄ×ų±ź“śČėµĆ£ŗ ![]() £¬
£¬
½āµĆ£ŗk=3£¬b=©3£®
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=3x©3£®
ÉčÖ±ĻßDEµÄ½āĪöŹ½ĪŖy=© ![]() x+n£¬½«µćDµÄ×ų±ź“śČėµĆ£ŗ©
x+n£¬½«µćDµÄ×ų±ź“śČėµĆ£ŗ© ![]() ”Į£Ø©4£©+n=5£¬½āµĆn=5©
”Į£Ø©4£©+n=5£¬½āµĆn=5© ![]() =
= ![]() £®
£®
”ąÖ±ĻßDEµÄ½āĪöŹ½ĪŖy=© ![]() x+
x+ ![]() £®
£®
½«y=3x©3Óėy=© ![]() x+
x+ ![]() ĮŖĮ¢½āµĆ£ŗx=2£¬y=3£®
ĮŖĮ¢½āµĆ£ŗx=2£¬y=3£®
”ąµćE×ų±źĪŖ£Ø2£¬3£©£®
ŅĄ¾ŻĮ½µć¼äµÄ¾ąĄė¹«Ź½æÉÖŖ£ŗBC=CE= ![]() £®
£®
”ßµćPÓėµćQ¹ŲÓŚµćB¶Ō³Ę£¬
”ąPB=BQ£®
ŌŚ”÷PCBŗĶ”÷QEBÖŠ 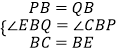 £¬
£¬
”ą”÷PCB”Õ”÷QEB£®
”ą”ĻBPC=”ĻQ£®
Ó֔ߔĻDEF+”ĻBPC=”ĻDBE£¬”ĻDEF=”ĻQEG£¬”ĻEGB=”ĻQ+”ĻQEG
”ą”ĻDBE=”ĻDGB£®
Ó֔ߔĻDBE+”ĻBDE=90”ć£¬
”ą”ĻDGB+”ĻBDG=90”ć£¬¼“”ĻPBD=90”ć£®
”ßD£Ø©4£¬5£©£¬B£Ø1£¬0£©£¬
”ąDM=NB£®
”ą”ĻDBN=45”ć£®
”ą”ĻPBM=45”ć£®
”ąPM=MB
ÉčµćPµÄ×ų±źĪŖ£Øa£¬a2+2a©3£©£¬ŌņBM=1©a£¬PM=©a2©2a+3£®
”ą1©a=©a2©2a+3£¬½āµĆ£ŗa=©2»ņa=1£ØÉįČ„£©£®
”ąµćPµÄ×ų±źĪŖ£Ø©2£¬3£©£®
”ąPC”ĪxÖį£®
”ß”ĻQ=”ĻBPC£¬
”ąEQ”ĪPC£®
”ąµćEÓėµćFµÄׯ×ų±źĻąĶ¬£®
½«y=3“śČėÅ×ĪļĻߵĽāĪöŹ½µĆ£ŗx2+2x©3=3£¬½āµĆ£ŗx=©1© ![]() »ņx=©1+
»ņx=©1+ ![]() £ØÉįČ„£©£®
£ØÉįČ„£©£®
”ąµćFµÄ×ų±źĪŖ£Ø©1 ![]() £¬3£©£®
£¬3£©£®
”ąEF=2©£Ø©1© ![]() £©=3+
£©=3+ ![]()
”¾½āĪö”æ£Ø1£©ĻČĒóµĆA”¢CĮ½µćµÄ×ų±ź£¬Č»ŗóĄūÓĆ“ż¶ØĻµŹż·ØĒó½ā¼“æÉ£»£Ø2£©ĻČĒóµĆABµÄ³¤£¬Č»ŗóŅĄ¾ŻS”÷ACD= ![]() SĖıߊĪACBD £¬ ĒóµĆAEµÄ³¤£¬æɵƵ½EµÄ×ų±źĪŖ£Ø©
SĖıߊĪACBD £¬ ĒóµĆAEµÄ³¤£¬æɵƵ½EµÄ×ų±źĪŖ£Ø© ![]() £¬0£©£¬ĄūÓĆ“ż¶ØĻµŹż·ØæÉĒóµĆCEµÄ½āĪöŹ½£¬Č»ŗóCEµÄ½āĪöŹ½ÓėÅ×ĪļĻߵĽāĪöŹ½ĮŖĮ¢æÉĒóµĆµćDµÄ×ų±ź£»£Ø3£©¹żµćD×÷DN”ĶxÖį£¬“¹×ćĪŖN£¬¹żµćP×÷PM”ĶxÖį£¬“¹×ćĪŖM£®ĻČĒóµĆBCŗĶDEµÄ½āĪöŹ½£¬“Ó¶ųæÉĒóµĆµćEµÄ×ų±ź£¬Č»ŗóæÉÖ¤Ć÷BC=BE£¬Č»ŗóæÉÖ¤Ć÷”÷PCB”Õ”÷QEB£¬µĆµ½”ĻBPC=”ĻQ£¬ŅĄ¾ŻĢāŅāæɵƵ½”ĻDBE=”ĻDGB£®½ÓĻĀĄ“£¬ŌŚÖ¤Ć÷”ĻPBD=90”ć£¬”ĻDBN=45”ć£¬Č»ŗóæÉĒóµĆ”ĻPBM=45”ć£¬ÉčµćPµÄ×ų±źĪŖ£Øa£¬a2+2a©3£©£¬ŌņBM=1©a£¬PM=©a2©2a+3Č»ŗóŅĄ¾ŻPM=MBæÉĒóµĆaµÄÖµ£¬ŌņæɵƵ½µćPµÄ×ų±ź£¬Č»ŗóæÉÖ¤Ć÷EF”ĪxÖį£¬×īŗ󽫵ćFµÄׯ×ų±ź“śČėÅ×ĪļĻߵĽāĪöŹ½æÉĒóµĆµćFµÄŗį×ų±ź£¬×īŗóŅĄ¾ŻEF=xE©xFĒó½ā¼“æÉ£®
£¬0£©£¬ĄūÓĆ“ż¶ØĻµŹż·ØæÉĒóµĆCEµÄ½āĪöŹ½£¬Č»ŗóCEµÄ½āĪöŹ½ÓėÅ×ĪļĻߵĽāĪöŹ½ĮŖĮ¢æÉĒóµĆµćDµÄ×ų±ź£»£Ø3£©¹żµćD×÷DN”ĶxÖį£¬“¹×ćĪŖN£¬¹żµćP×÷PM”ĶxÖį£¬“¹×ćĪŖM£®ĻČĒóµĆBCŗĶDEµÄ½āĪöŹ½£¬“Ó¶ųæÉĒóµĆµćEµÄ×ų±ź£¬Č»ŗóæÉÖ¤Ć÷BC=BE£¬Č»ŗóæÉÖ¤Ć÷”÷PCB”Õ”÷QEB£¬µĆµ½”ĻBPC=”ĻQ£¬ŅĄ¾ŻĢāŅāæɵƵ½”ĻDBE=”ĻDGB£®½ÓĻĀĄ“£¬ŌŚÖ¤Ć÷”ĻPBD=90”ć£¬”ĻDBN=45”ć£¬Č»ŗóæÉĒóµĆ”ĻPBM=45”ć£¬ÉčµćPµÄ×ų±źĪŖ£Øa£¬a2+2a©3£©£¬ŌņBM=1©a£¬PM=©a2©2a+3Č»ŗóŅĄ¾ŻPM=MBæÉĒóµĆaµÄÖµ£¬ŌņæɵƵ½µćPµÄ×ų±ź£¬Č»ŗóæÉÖ¤Ć÷EF”ĪxÖį£¬×īŗ󽫵ćFµÄׯ×ų±ź“śČėÅ×ĪļĻߵĽāĪöŹ½æÉĒóµĆµćFµÄŗį×ų±ź£¬×īŗóŅĄ¾ŻEF=xE©xFĒó½ā¼“æÉ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖĖıߊĪABCD£¬”ĻABC=45”ć£¬”ĻC=”ĻD=90”ć£¬ŗ¬30”ć½Ē£Ø”ĻP=30”ć£©µÄÖ±½ĒČż½Ē°åPMN£ØČēĶ¼£©ŌŚĶ¼ÖŠĘ½ŅĘ£¬Ö±½Ē±ßMN”ĶBC£¬¶„µćM”¢N·Ö±šŌŚ±ßAD”¢BCÉĻ£¬ŃÓ³¤NMµ½µćQ£¬Ź¹QM=PB£®ČōBC=10£¬CD=3£¬Ōņµ±µćM“ÓµćAĘ½Ņʵ½µćDµÄ¹ż³ĢÖŠ£¬µćQµÄŌĖ¶ÆĀ·¾¶³¤ĪŖ £® 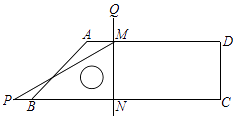
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»ÓꓬÓÉĪ÷Ķł¶«ŗ½ŠŠ£¬ŌŚAµć²āµĆŗ£µŗCĪ»ÓŚ±±Ę«¶«60”ćµÄ·½Ļņ£¬Ē°½ų40ŗ£Ąļµ½“ļBµć£¬“ĖŹ±£¬²āµĆŗ£µŗCĪ»ÓŚ±±Ę«¶«30”ćµÄ·½Ļņ£¬Ōņŗ£µŗCµ½ŗ½ĻßABµÄ¾ąĄėCDŹĒ£Ø £©
A.20ŗ£Ąļ
B.40ŗ£Ąļ
C.20 ![]() ŗ£Ąļ
ŗ£Ąļ
D.40 ![]() ŗ£Ąļ
ŗ£Ąļ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬µćD”¢E”¢F·Ö±šŌŚAB”¢BC”¢AC±ßÉĻ£¬ĒŅBE=CF£¬BD=CE.
£Ø1£©ĒóÖ¤£ŗ”÷DEFŹĒµČŃüČż½ĒŠĪ£»
£Ø2£©µ±”ĻA=40”揱£¬Ēó”ĻDEFµÄ¶ČŹż£»

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³ÖŠŃ§ĪŖĮĖĀĢ»ÆŠ£Ō°,¼Ę»®¹ŗĀņŅ»ÅśéÅŹ÷ŗĶĻćÕĮŹ÷,¾ŹŠ³”µ÷²é,éÅŹ÷µÄµ„¼Ū±ČĻćÕĮŹ÷ÉŁ20ŌŖ,¹ŗĀņ3æĆéÅŹ÷ŗĶ2æĆĻćÕĮŹ÷¹²Šč340ŌŖ.
(1)éÅŹ÷ŗĶĻćÕĮŹ÷µÄµ„¼Ūø÷ŹĒ¶ąÉŁ?
(2)øł¾ŻŃ§Š£Źµ¼ŹĒéæö,Šč¹ŗĀņĮ½ÖÖŹ÷Ćē¹²150æĆ,×Ü·ŃÓĆ²»³¬¹ż10840ŌŖ,ĒŅ¹ŗĀņĻćÕĮŹ÷µÄæĆŹż²»ÉŁÓŚéÅŹ÷µÄ1.5±¶,ĒėÄćĖćĖćøĆŠ£±¾“Ī¹ŗĀņéÅŹ÷ŗĶĻćÕĮŹ÷¹²ÓŠÄļøÖÖ·½°ø.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øö²»ĶøĆ÷µÄ“ü×Ó֊װӊŗŚĒņĮ½øö£¬°×ĒņČżøö£¬ÕāŠ©Š”Ēņ³żŃÕÉ«ĶāĪŽĘäĖūĒų±š£¬“Ó“ü×ÓÖŠĖ껜ƞ³öŅ»øöŠ”Ēņŗ󣬷ŻŲ²¢Ņ”ŌČ£¬ŌŁĖ껜ƞ³öŅ»øöŠ”Ēņ£¬ŌņĮ½“ĪĆž³öµÄŠ”Ēņ¶¼ŹĒŗŚĒņµÄøÅĀŹĪŖ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
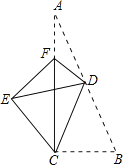
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB=90”ć£¬AB=2![]() £¬BC=2£¬µćDĪŖŠ±±ßABµÄÖŠµć£¬Į¬½ÓCD£¬½«”÷BCDŃŲCD·ÕŪ£¬Ź¹µćBĀäŌŚµćE“¦£¬µćFĪŖÖ±½Ē±ßACÉĻŅ»µć£¬Į¬½ÓDF£¬½«”÷ADFŃŲDF·ÕŪ£¬Ź¹µćAÓėµćEÖŲŗĻ£¬ĒóÕŪŗŪDFµÄ³¤£®
£¬BC=2£¬µćDĪŖŠ±±ßABµÄÖŠµć£¬Į¬½ÓCD£¬½«”÷BCDŃŲCD·ÕŪ£¬Ź¹µćBĀäŌŚµćE“¦£¬µćFĪŖÖ±½Ē±ßACÉĻŅ»µć£¬Į¬½ÓDF£¬½«”÷ADFŃŲDF·ÕŪ£¬Ź¹µćAÓėµćEÖŲŗĻ£¬ĒóÕŪŗŪDFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”÷ABCÖŠ£¬”ĻACB=90”ć£¬”ĻA=¦Į£¬ŅŌCĪŖÖŠŠÄ½«”÷ABCŠż×Ŗ¦Č½Ēµ½”÷A1B1C£ØŠż×Ŗ¹ż³ĢÖŠ±£³Ö”÷ABCµÄŠĪד“󊔲»±ä£©BµćĒ”ĀäŌŚA1B1ÉĻ£¬ČēĶ¼£¬ŌņŠż×Ŗ½Ē¦ČµÄ“óŠ”ĪŖ£Ø £© 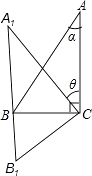
A.¦Į+10”ć
B.¦Į+20”ć
C.¦Į
D.2¦Į
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
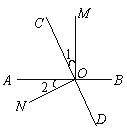
”¾ĢāÄæ”æČēĶ¼,Ö±ĻßAB£¬CDĻą½»ÓŚOµć£¬OM”ĶAB.
£Ø1£©Čō”Ļ1=”Ļ2£¬Ēó”ĻNOD£»
£Ø2£©Čō”Ļ1=![]() ”ĻBOC£¬Ēó”ĻAOCÓė”ĻMOD.
”ĻBOC£¬Ēó”ĻAOCÓė”ĻMOD.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com