
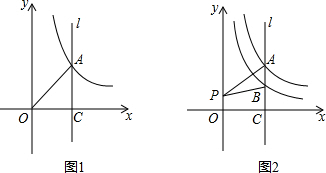
分析 (1)首先设点A(a,b),则ab=m,继而可求得△OAC的面积;
(2)①首先连接OA,OB,由(1)可得S△OAC=$\frac{1}{2}$m,S△OBC=$\frac{1}{2}$n,继而可得S△PAB=S△OAB=S△OAC-S△OBC;
②首先作点B关于y轴的对称点B′,作直线AB′交于y轴于点D,可得当点P于点D重合时,△PAB的周长最小,由点A的坐标为(2,2),且点B为AC的中点,可求得点B与点B′的坐标,继而可求得直线对应的函数解析式;然后由勾股定理求得AB′的长,继而可得△PAB的周长=AB′+AB.
解答  解:(1)设点A(a,b),则ab=m,
解:(1)设点A(a,b),则ab=m,
∴S△OAC=$\frac{1}{2}$ab=$\frac{1}{2}$m;
(2)①如答图1,连接OA,OB,
则S△OAC=$\frac{1}{2}$m,S△OBC=$\frac{1}{2}$n,
∴S△PAB=S△OAB=S△OAC-S△OBC=$\frac{1}{2}$m-$\frac{1}{2}$n=$\frac{1}{2}$(m-n);
②如答图2,作点B关于y轴的对称点B′,作直线AB′交于y轴于点D,当点P于点D重合时,△PAB的周长最小,
∵点A的坐标为(2,2),且点B为AC的中点,
∴点B的坐标为:(2,1),点B′的坐标为:(-2,1),
设直线AP对应的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{-2k+b=1}\\{2k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴直线AP对应的解析式为:y=$\frac{1}{4}$x+$\frac{3}{2}$,
∵AB=2-1=1,BB′=2-(-2)=4,
∴在Rt△ABB′中,AB′=$\sqrt{A{B}^{2}+BB{′}^{2}}$=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
∴△PAB的周长为:PA+PB+AB=PA+PB′+AB=AB′+AB=$\sqrt{17}$+1.
点评 此题属于反比例函数综合题,考查了反比例函数k的几何意义、待定系数法求函数的解析式以及最短路径问题.注意掌握辅助线的作法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-2 | B. | x≤1 | C. | -2≤x≤1 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
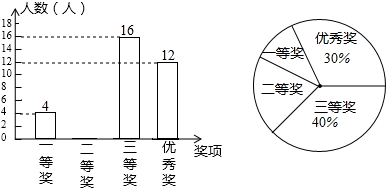
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
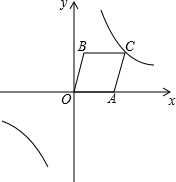 如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y=$\frac{k}{x}$的图象经过点C.
如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y=$\frac{k}{x}$的图象经过点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com