
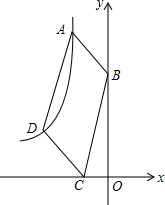
 如图,在平面直角坐标系xOy中,已知A(1-$\sqrt{5}$,1+$\sqrt{5}$),B(0,1),双曲线y=$\frac{k}{x}$经过?ABCD的顶点A、D,求D点的坐标.
如图,在平面直角坐标系xOy中,已知A(1-$\sqrt{5}$,1+$\sqrt{5}$),B(0,1),双曲线y=$\frac{k}{x}$经过?ABCD的顶点A、D,求D点的坐标. 分析 由A点坐标可求得反比例函数解析式,作AE⊥y轴于E,DF⊥x轴于F,由条件可证明△AEB≌△CFD,可求得CF,则可求得D点纵坐标,再把D点纵坐标代入可求得D点坐标.
解答  解:
解:
如图,作AE⊥y轴于E,DF⊥x轴于F,延长AD交x轴于点N,延长DA,
∵A点在双曲线y=$\frac{k}{x}$图象上,
∴k=(1-$\sqrt{5}$)×(1+$\sqrt{5}$)=1-5=-4,
∴反比例函数解析式为y=-$\frac{4}{x}$,
∵四边形ABCD为平行四边形,
∴AD∥BC,AB=DC,
∴∠MAE=∠DNC=∠BCO,且∠BAD=∠DCB,
∵∠MAE+∠EAB+∠DAB=∠DCF+∠DCB+∠BCO=180°,
∴∠DCF=∠EAB,
在△AEB和△CFD中
$\left\{\begin{array}{l}{∠AEB=∠DFC}\\{∠EAB=∠DCF}\\{AB=DC}\end{array}\right.$
∴△AEB≌△CFD(AAS),
∴DF=BE,
∴A(1-$\sqrt{5}$,1+$\sqrt{5}$),B(0,1),
∴OB=1,OE=1+$\sqrt{5}$,
∴BE=OE-OB=$\sqrt{5}$,
∴DF=$\sqrt{5}$,
∴D点纵坐标为$\sqrt{5}$,
又点D在双曲线上,
∴$\sqrt{5}$=-$\frac{4}{x}$,解得x=-$\frac{4\sqrt{5}}{5}$,
∴D点坐标为(-$\frac{4\sqrt{5}}{5}$,$\sqrt{5}$).
点评 本题主要考查函数图象上点的坐标,利用条件证得△AEB≌△CFD求得DF的长是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2016-2017学年广西北海市七年级上学期期末教学质量检测数学试卷(解析版) 题型:单选题
如图,  ,
,  是数轴上的两个有理数,下面说法中正确的是( )
是数轴上的两个有理数,下面说法中正确的是( )

A.  B.
B.  C.
C.  D. a+b<0
D. a+b<0
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
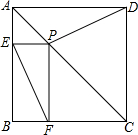 如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为( )
如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为( )| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D是边BC中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点P在边AB上,EF∥BC.
如图,在△ABC中,点D是边BC中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点P在边AB上,EF∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a2-a2+ab2的次数是2次 | B. | $\frac{{2{x^2}}}{x}$是分式 | ||
| C. | $\frac{a-1}{a+1}=-1$ | D. | $\frac{{{a^2}-ab}}{{{b^2}-ab}}$=$\frac{a^2}{b^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知,如图所示的一张三角形纸片ABC,边AB的长为20cm,AB边上的高为25cm,在三角形纸片ABC中从下往上依次裁剪去宽为4cm的矩形纸条,若剪得的其中一张纸条是正方形,那么这张正方形纸条是( )
已知,如图所示的一张三角形纸片ABC,边AB的长为20cm,AB边上的高为25cm,在三角形纸片ABC中从下往上依次裁剪去宽为4cm的矩形纸条,若剪得的其中一张纸条是正方形,那么这张正方形纸条是( )| A. | 第4张 | B. | 第5张 | C. | 第6张 | D. | 第7张 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com