
【题目】已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
(1)若AP=5,AB=![]() BC,求矩形ABCD的面积;
BC,求矩形ABCD的面积;
(2)若CD=PM,试判断线段AC、AP、PN之间的关系,并证明.

【答案】(1)15;(2)AC=AP+PN,证明详见解析.
【解析】
(1)由等腰直角三角形的性质可得AC=![]() AP=5
AP=5![]() ,由勾股定理可求AB=
,由勾股定理可求AB=![]() ,BC=3
,BC=3![]() ,即可求矩形ABCD的面积;
,即可求矩形ABCD的面积;
(2)由矩形的性质可得∠ADC=∠APC=90°,可证点A,点C,点D,点P四点共圆,可得∠PDA=∠PCA=45°,∠PCD=∠PAD,∠DPC=∠DCA,由“ASA”可证△ADE≌△ADC,△PAN≌△PEC,可得AC=AE,PN=PE,即可得结论.
解:(1)∵AP=PC,AP⊥PC,
∴AC=![]() AP=5
AP=5![]()
∵AB2+BC2=AC2,AB=![]() BC,
BC,
∴AB=![]() ,BC=3
,BC=3![]()
∴S四边形ABCD=AB×BC=15
(2)AC=AP+PN
如图.延长AP,CD交于点E
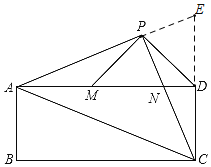
∵AP=PC,AP⊥PC,
∴∠APC=90°,∠PAC=∠PCA=45°
∵四边形ABCD是矩形
∴∠ADC=90°,
∴∠ADC=∠APC
∴点A,点C,点D,点P四点共圆
∴∠PDA=∠PCA=45°,∠PCD=∠PAD,∠DPC=∠DCA,
∵PM⊥PD
∴∠PMD=∠PDM=45°
∴PM=PD,且PM=CD
∴PD=CD,
∴∠DPC=∠DCP
∴∠PAD=∠DAC,且AD=AD,∠ADE=∠ADC=90°
∴△ADE≌△ADC(ASA)
∴AC=AE,
∵AP=PC,∠APC=∠EPC=90°,∠PCE=∠PAD
∴△PAN≌△PEC(ASA)
∴PN=PE
∴AC=AE=AP+PE=AP+PN


科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
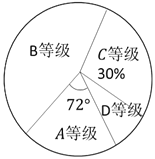
【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查了部分学生的数学成绩,并将抽样的数据进行了如下整理.
(1)填空![]() _______,
_______,![]() _______,数学成绩的中位数所在的等级_________.
_______,数学成绩的中位数所在的等级_________.
(2)如果该校有1200名学生参加了本次模拟测,估计![]() 等级的人数;
等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A级学生的数学成绩的平均分数.
①如下分数段整理样本
等级等级 | 分数段 | 各组总分 | 人数 |
|
|
| 4 |
|
| 843 |
|
|
| 574 |
|
|
| 171 | 2 |
②根据上表绘制扇形统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
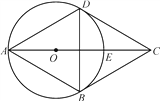
【题目】已知:如图,四边形ABCD为菱形,△ABD的外接圆⊙O与CD相切于点D,交AC于点E.
(1)判断⊙O与BC的位置关系,并说明理由;
(2)若CE=2,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,1),B(1,0),PQ是直线y=x上的一条动线段且PQ=![]() (Q在P的下方),当AP+PQ+QB取最小值时,点Q坐标为______.
(Q在P的下方),当AP+PQ+QB取最小值时,点Q坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有 (写出所有正确结论的序号)
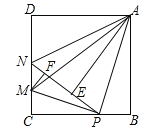
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为![]() ;
;
⑤当△ABP≌△ADN时,BP=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
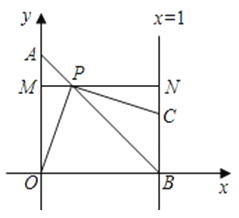
【题目】如图,以 ![]() 为原点的直角坐标系中,
为原点的直角坐标系中, ![]() 点的坐标为(0, 1),直线
点的坐标为(0, 1),直线 ![]() 交
交![]() 轴于点
轴于点![]() .
.![]() 为线段
为线段![]() 上一动点,作直线
上一动点,作直线![]() ,交直线
,交直线![]() 于点
于点![]() . 过
. 过![]() 点作直线
点作直线![]() 平行于
平行于![]() 轴,交
轴,交![]() 轴于点
轴于点 ![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)当点![]() 在第一象限时,求证:
在第一象限时,求证:![]() ;
;
(2)当点![]() 在第一象限时,设
在第一象限时,设![]() 长为
长为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,请求出
,请求出![]() 与
与![]() 间的函数关系式,并写出自变量
间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 也随之在直线
也随之在直线![]() 上移动,
上移动,![]() 是否可能成为等腰三角形?如果可能,求出所有能使
是否可能成为等腰三角形?如果可能,求出所有能使![]() 成为等腰直角三角形的点
成为等腰直角三角形的点![]() 的坐标;如果不可能,请说明理由.
的坐标;如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 x1、x2是一元二次方程4kx2﹣4kx+k+1=0的两个实数根.
(1)求k的取值范围.
(2)是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣![]() 成立?若存在求出k的值;若不存在,请说明理由.
成立?若存在求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com