
【题目】下列说法正确的是( )
A.一个三角形的三边长分别为:a,b,c,且a2﹣b2=c2,则这个三角形是直角三角形
B.三边长度分别为1,1,![]() 的三角形是直角三角形,且1,1,
的三角形是直角三角形,且1,1,![]() 是组勾股数
是组勾股数
C.三边长度分别是12,35,36的三角形是直角三角形
D.在一个直角三角形中,有两边的长度分别是3和5,则另一边的长度一定是4
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.

(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用三角尺可按如图所示的方法画角平分线:已知∠AOB,把一个三角尺的一个顶点放在点O处,一条直角边放在OB上,过直角顶点C作OB的垂线DC;再用同样的方法作OA的垂线EF, EF与DC交于点P.作射线OP,则OP即为∠AOB的平分线.这样作图的依据是构造两个三角形全等,由作法可知,△EPO≌△CPO的依据是( ).
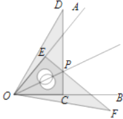
A.SASB.HLC.ASAD.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1 、A2 、A3是抛物线y=x2上三点, A1B1 、A2B2 、A3B3 分别是垂直于x轴,垂足为B1 、B2 、B3 ,直线A2B2交线段A1A3于点C,若A1 、A2 、A3 三点的横坐标依次为1、2、3,则线段CA2的长为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区环保局在检查该地区某铝厂时发现,该厂污水严重影响周围环境,要求做定期整改,据估测,该厂年排放污水量为36万吨,接到通知后,该厂决定分两期投入治理,一方面对排放的污水进行处理,同时使得处理后的污水年排放量减少到17.64万吨,如果每期治理中污水减少的百分率相同.
(1)问每期减少的百分率为多少?
(2)如果第一期治理中每减少排放1万吨污水,需投入2万元,第二期每减少排放1万吨污水,需投入3万元,问预计两期治理共需多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中菲黄岩岛争端持续,我海监船加大黄岩岛附近海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,黄岩岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向黄岩岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
(1)请用直尺和圆规作出C处的位置;

(2)求我国海监船行驶的航程BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)所示).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成的记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若EF=4,则S1+S2+S3的值是( )
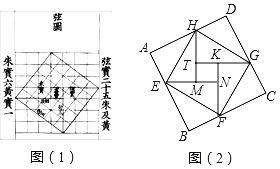
A.32B.38C.48D.80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个等腰直角△ABC和△CDE中,∠ACB=∠DCE=90°.
(1)观察猜想如图1,点E在BC上,线段AE与BD的数量关系,位置关系.
(2)探究证明把△CDE绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;
(3)拓展延伸:把△CDE绕点C在平面内自由旋转,若AC=BC=13,DE=10,当A、E、D三点在直线上时,请直接写出AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com