
【题目】有这样一个问题:探究同一坐标系中系数互为倒数的正、反比例函数![]() 与
与![]() 的图象性质
的图象性质![]() 小明根据学习函数的经验,对这两个函数当
小明根据学习函数的经验,对这两个函数当![]() 时的图象性质进行了探究
时的图象性质进行了探究![]() 设函数
设函数![]() 与
与![]() 图象的交点为A、
图象的交点为A、![]() 下面是小明的探究过程:
下面是小明的探究过程:
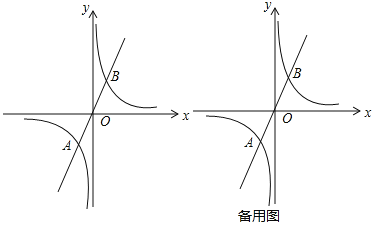
(1)如图所示,若已知A的坐标为![]() ,则B点的坐标为______.
,则B点的坐标为______.
(2)若A的坐标为![]() ,P点为第一象限内双曲线上不同于点B的任意一点.
,P点为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点![]() 求证:
求证:![]() .
.
证明过程如下:设![]() ,直线PA的解析式为
,直线PA的解析式为![]() .
.
则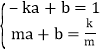
解得![]()
所以,直线PA的解析式为______.
请把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为![]() 时,判断
时,判断![]() 的形状,并用k表示出
的形状,并用k表示出![]() 的面积.
的面积.
【答案】(1)![]() ;(2)①
;(2)①![]() ,
,![]() ,
,![]() ;②直角三角形,
;②直角三角形,![]() 或
或![]() .
.![]()
【解析】
(1)根据正、反比例函数图象的对称性结合点A的坐标即可得出点B的坐标;
(2)①设P(m,![]() ),根据点P、A的坐标利用待定系数法可求出直线PA的解析式,利用一次函数图象上点的坐标特征可求出点M的坐标,过点P作PH⊥x轴于H,由点P的坐标可得出点H的坐标,进而即可求出MH的长度,同理可得出HN的长度,再根据等腰三角形的三线合一即可证出PM=PN;
),根据点P、A的坐标利用待定系数法可求出直线PA的解析式,利用一次函数图象上点的坐标特征可求出点M的坐标,过点P作PH⊥x轴于H,由点P的坐标可得出点H的坐标,进而即可求出MH的长度,同理可得出HN的长度,再根据等腰三角形的三线合一即可证出PM=PN;
②根据①结合PH、MH、NH的长度,可得出△PAB为直角三角形,分k>1和0<k<1两种情况,利用分割图形求面积法即可求出△PAB的面积.
解:(1)由正、反比例函数图象的对称性可知,点A、B关于原点O对称,
![]() 点的坐标为
点的坐标为![]() ,
,
![]() 点的坐标为
点的坐标为![]() .
.
故答案为:![]() .
.
(2)①证明过程如下,
设![]() ,直线PA的解析式为
,直线PA的解析式为![]() .
.
则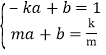 ,
,
解得: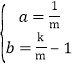 ,
,
![]() 直线PA的解析式为
直线PA的解析式为![]() .
.
当![]() 时,
时,![]() ,
,
![]() 点的坐标为
点的坐标为![]() .
.
过点P作![]() 轴于H,如图1所示,
轴于H,如图1所示,
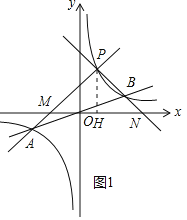
![]() 点坐标为
点坐标为![]() ,
,
![]() 点的坐标为
点的坐标为![]() ,
,
![]() .
.
同理可得:![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
故答案为:![]() ,
,![]() ,
,![]() ;
;
②由(2)①可知,在![]() 中,
中,![]() ,
,
![]() 为等腰三角形,且
为等腰三角形,且![]() .
.
当P点坐标为![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
![]() 为直角三角形.
为直角三角形.
当![]() 时,如图1,
时,如图1,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
当![]() 时,
时,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
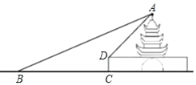
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
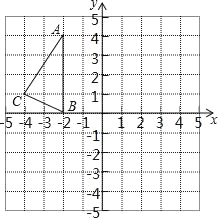
【题目】如图,在正方形网格中,△ABC的三个顶点都在格点上,点A,B,C的坐标分别为(﹣2,4)、(﹣2,0)、(﹣4,1),将△ABC绕原点O旋转180度得到△A1B1C1.平移△ABC得到△A2B2C2,使点A移动到点A2(0,2),结合所给的平面直角坐标系解答下列问题:
(1)请画出△A1B1C1;
(2)请直接写出B2的坐标 C2的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
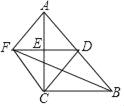
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别是边AB、AC的中点,延长DE至F,使得AF∥CD,连接BF、CF.
(1)求证:四边形AFCD是菱形;
(2)当AC=4,BC=3时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
(1)请你为m选取一个合适的整数,使得到的方程有两个不相等的实数根;
(2)设![]() 、
、![]() 是
是![]() 中你所得到的方程的两个实数根,求:
中你所得到的方程的两个实数根,求:![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
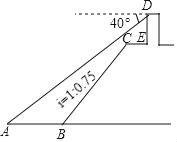
【题目】如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
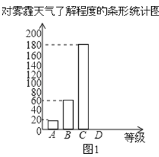
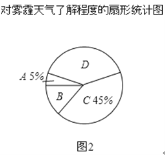
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0,其中正确的命题是( )
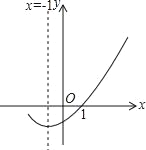
A. ①②③B. ①③C. ①④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
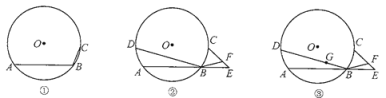
【题目】问题1如图①点A、B、C在⊙O上,且∠ABC=120°,⊙O的半径是3.求弧AC的长.
问题2如图②点A、B、C、D在⊙![]() 上,且弧AD=弧BC,E是AB的延长线上的
上,且弧AD=弧BC,E是AB的延长线上的![]() .
.
(1)设BD=nBF,则n=________;
(2)如图③若G是线段BD上的一个点,且![]() .试探究,在⊙
.试探究,在⊙![]() 上是否存在点P (B除外)使PG=PF?为什么?
上是否存在点P (B除外)使PG=PF?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com