Question

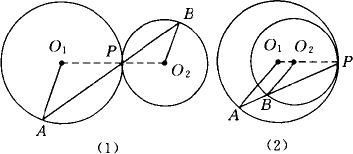
如下图所示，⊙O₁和⊙O₂相切于P点，过P的直线交⊙O₁于A，交⊙O₂于B．求证O₁A∥O₂B．

Answer 1

答案：
解析：

证明：①如图(1)所示，连接O1O2，则O1O2必过切点P， 　　∵O1A＝O1P，∴∠A＝∠O1PA， 　　又O2B＝O2P，∴∠B＝∠O2PB， 　　又∠O1PA＝∠O2PB，∴∠A＝∠B，∴O1A∥O2B． 　　②如图(2)所示，连接O1O2并延长， 　　则O1O2的延长线必过点P， 　　∵O1A＝O1P，∴∠A＝∠P， 　　又∵O2B＝O2P，∴∠O2BP＝∠P， 　　∴∠A＝∠O2BP，∴O1A∥O2B． 　　分析：上图给出了内切、外切两种情况，因此要分两种情况进行证明．①如图(1)所示，连接O1O2，则O1O2必过切点P；②如图(2)所示，连接O1O2并延长，必过切点P．要证O1A∥O2B，在①中只要证∠A＝∠B即可，在②中，只要证∠A＝∠O2BP即可． 　　小结：由于相切两圆的连心线经过切点，所以涉及两圆相切的问题时，作连心线(或圆心距)是一种重要的添加辅助线的方法．