
分析 (1)方程有实数根,则△≥0,建立关于n的不等式,求出m的取值范围.
(2)由三角形是等腰三角形,得到两种情况①a=2或b=2,②a=b;①当a=2,或b=2时,得到方程的根x=2,把x=2代入x2-6x+n-1=0即可得到结果;②当a=b时,方程x2-6x+n-1=0有两个相等的实数根,由△=(-6)2-4(n-1)=0可的结果.
解答 解:(1)由题意,得
△=b2-4ac=(-6)2-4(n-1)=40-4n,
∵a、b是关于x的一元二次方程x2-6x+n-1=0的两根,
∴40-4n≥0.
∴n≤10.
(2))∵三角形是等腰三角形,
∴①a=2或b=2,②a=b两种情况,
①当a=2,或b=2时,
∵a,b是关于x的一元二次方程x2-6x+n-1=0的两根,
∴x=2,
把x=2代入x2-6x+n-1=0得,22-6×2+n-1=0,
解得:n=9,
当n=9,方程的两根是2和4,而2,4,2不能组成三角形,
故n=9不合题意,舍去;
②当a=b时,方程x2-6x+n-1=0有两个相等的实数根,
∴△=(-6)2-4(n-1)=0
解得:n=10,
综上所述,n=10.
点评 本题考查了等腰三角形的性质,一元二次方程的根,一元二次方程根的判别式.解题时,注意分类讨论思想的应用.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知点A(0,8),点B(6,0),点P从B点以每秒1个单位的速度沿着BA方向出发,当点P运动到点A时停止,若设点P运动时间为t秒.
如图,在平面直角坐标系中,已知点A(0,8),点B(6,0),点P从B点以每秒1个单位的速度沿着BA方向出发,当点P运动到点A时停止,若设点P运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮他确定C地的位置吗?
有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮他确定C地的位置吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
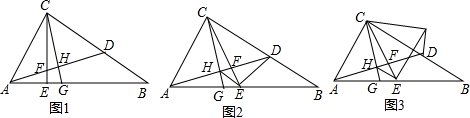
 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:| A. | 只有① | B. | ①②④ | C. | ①②③④ | D. | ①②④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
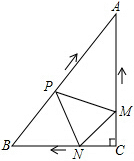 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t<2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t<2.5).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com