
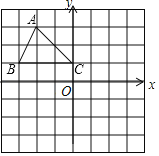
【题目】如图,在平面直角坐标系中,△ABC三个顶点都在格点上,点A,B,C的坐标分别为A(﹣2,3),B(﹣3,1),C(0,1)请解答下列问题:
(1)△ABC与△A1B1C1关于原点O成中心对称,画出△A1B1C1并直接写出点A的对应点A1的坐标;
(2)画出△ABC绕点C顺时针旋转90°后得到的△A2B2C,并求出线段AC旋转时扫过的面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=ax+b的图象与反比例函数y2=![]() 的图象相交于A、B两点,坐标分别为(—2,4)、(4,—2).
的图象相交于A、B两点,坐标分别为(—2,4)、(4,—2).
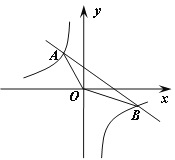
(1)求两个函数的解析式;
(2)求△AOB的面积;
(3)直线AB上是否存在一点P(A除外),使△ABO与以B﹑P、O为顶点的三角形相似?若存在,直接写出顶点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() ,
,![]() ,如果
,如果![]() ,则称
,则称![]() 与
与![]() 互为“
互为“![]() 距点”.例如:点
距点”.例如:点![]() ,点
,点![]() ,由
,由![]() ,可得点
,可得点![]() 与
与![]() 互为“
互为“![]() 距点”.
距点”.
(1)在点![]() ,
,![]() ,
,![]() 中,原点
中,原点![]() 的“
的“![]() 距点”是_____(填字母);
距点”是_____(填字母);
(2)已知点![]() ,点
,点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() .
.
①当![]() 时,直线
时,直线![]() 上点
上点![]() 的“
的“![]() 距点”的坐标为_____;
距点”的坐标为_____;
②若直线![]() 上存在点
上存在点![]() 的“
的“![]() 点”,求
点”,求![]() 的取值范围.
的取值范围.
(3)已知点![]() ,
,![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,若在线段
,若在线段![]() 上存在点
上存在点![]() ,在
,在![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 与点
与点![]() 互为“
互为“![]() 距点”,直接写出
距点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年第七届世界军人运动会(7thCISMMilitaryWorldGames)于2019年10月18日至27日在中国武汉举行,这是中国第一次承办综合性国际军事赛事,也是继北京奥运会后,中国举办的规模最大的国际体育盛会.某射击运动员在一次训练中射击了10次,成绩如图所示.下列结论中不正确的有( )个
①众数是8;②中位数是8;③平均数是8;④方差是1.6.
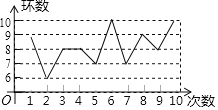
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
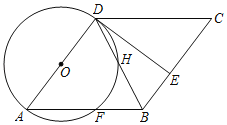
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
(1)求证:△DAF≌△DCE.
(2)求证:DE是⊙O的切线.
(3)若BF=2,DH=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
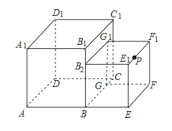
【题目】棱长分别为![]() 的两个正方体如图放置,点
的两个正方体如图放置,点![]() ,
,![]() ,
,![]() 在同一直线上,顶点
在同一直线上,顶点![]() 在棱上,点
在棱上,点![]() 是
是![]() 的中点.一只蚂蚁要沿着正方体的表面从点
的中点.一只蚂蚁要沿着正方体的表面从点![]() 爬到点
爬到点![]() ,它爬行的最短距离是__________.
,它爬行的最短距离是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面四个实验中,实验结果概率最小的是( )

A.如(1)图,在一次实验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,估计出的钉尖朝上的概率
B.如(2)图,是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率
C.如(3)图,有一个小球在的地板上自由滚动,地板上的每个格都是边长为1的正方形,则小球在地板上最终停留在黑色区域的概率
D.有7张卡片,分别标有数字1,2,3,4,6,8,9,将它们背面朝上洗匀后,从中随机抽出一张,抽出标有数字“大于6”的卡片的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
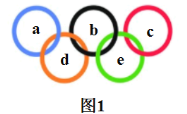
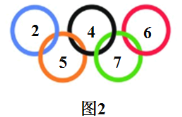
【题目】问题:如图1,五环图案内写有5个正整数![]() ,请对5个整数作规律探索,找出同时满足以下3个条件的数;①
,请对5个整数作规律探索,找出同时满足以下3个条件的数;①![]() 是三个连续偶数
是三个连续偶数![]() ;②
;②![]() 是两个连续奇数
是两个连续奇数![]() ;③满足
;③满足![]() .尝试: 取
.尝试: 取![]() ,如图2,
,如图2,![]() ,5个正整数满足要求;
,5个正整数满足要求;
(1)取![]() ,能写出满足条件的5个正整数吗?如果能,写出
,能写出满足条件的5个正整数吗?如果能,写出![]() 的值;如果不能,说明理由.
的值;如果不能,说明理由.
(2)取![]() ,能写出满足条件的5个正整数吗?如果能,写出
,能写出满足条件的5个正整数吗?如果能,写出![]() 的值;如果不能,说明理由.
的值;如果不能,说明理由.
(3)猜想: 若5个正整数能满足上述三个要求,偶数![]() 具备怎样的条件?
具备怎样的条件?
(4)概括: 现有5个正整数![]() 满足问题中的三个条件,请用含
满足问题中的三个条件,请用含![]() 的代数式表示
的代数式表示![]() (设
(设![]() 为正整数).
为正整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com