
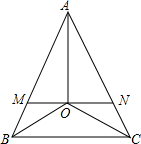
 (1)如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB、AC于M、N,图中有几个等腰三角形?
(1)如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB、AC于M、N,图中有几个等腰三角形?分析 (1)根据AB=AC,AM=AN,OB=OC即可得出等腰三角形;
(2)根据等腰三角形的性质得到∠ABC=∠ACB,根据平行线的性质得到∠AMN=∠ABC=∠ANM=∠ACB,于是得到AM=AN,BM=CN,由于BO是∠B的角平分线,得到∠MBO=∠OBC,推出∠MBO=∠MOB,得到BM=OM,等量代换得到ON=CN,∠NCO=∠OBC,即可得到结论.
解答 (1)解:等腰三角形有△ABC、△OBC、△MBO、△NCO、△AMN等;
(2)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵MN∥BC,
∴∠AMN=∠ABC=∠ANM=∠ACB,
∴AM=AN,
∴BM=CN,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∵BO是∠B的角平分线,
∴∠MBO=∠OBC,
∴∠MBO=∠MOB,
∴BM=OM,
∵OM=ON,
∴ON=CN,
∴∠NOC=∠NCO,
∴∠NCO=∠OBC,
∴CO是∠C的角平分线.
点评 本题考查了等腰三角形的判定与性质,全等三角形的判定与性质,角平分线的定义,平行线的性质,综合性较强,但难度不大,仔细分析图形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com