
 如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+b的图象与x轴交于点为A(-4$\sqrt{3}$,0),与y轴交于点为B.
如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+b的图象与x轴交于点为A(-4$\sqrt{3}$,0),与y轴交于点为B.分析 (1)利用待定系数法求得直线AB的解析式,然后求得B的坐标,利用三角形函数求得∠ABO的度数;
(2)四边形ABCD是直角梯形,分类讨论①CD⊥AD,AB是底边时,②AD∥BC,CD⊥AD时.
解答 解:(1)把(-4$\sqrt{3}$,0)代入y=-$\frac{\sqrt{3}}{3}$x+b得4+b=0,
解得:b=-4,
则函数的解析式是y=-$\frac{\sqrt{3}}{3}$x-4,
当x=0时,y=-4,则OB=4,B的坐标是(0,-4),
tan∠BAO=$\frac{OB}{OA}$=$\frac{4}{4\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠BAO=30°;
(2)四边形ABCD是直角梯形,
①CD⊥AD,AB是底边.
设过A且与AB垂直的直线的解析式是y=$\sqrt{3}$x+c,
把(-4$\sqrt{3}$,0)代入得:-12+c=0,
解得:c=12,
则直线解析式是y=$\sqrt{3}$x+12,
过C与AB平行的直线解析式是y=-$\frac{\sqrt{3}}{3}$x+2,
则根据题意得:$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+2}\\{y=\sqrt{3}x+12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-\frac{5\sqrt{3}}{2}}\\{y=\frac{9}{2}}\end{array}\right.$,
则D的坐标是(-$\frac{5\sqrt{3}}{2}$,$\frac{9}{2}$);
②AD∥BC,CD⊥AD时,由于A(-4$\sqrt{3}$,0),C(0,2),则可知D(-4$\sqrt{3}$,2).
综上D(-$\frac{5\sqrt{3}}{2}$,$\frac{9}{2}$)或(-4$\sqrt{3}$,2).
点评 本题考查了待定系数法求函数的解析式,正确确定D点的位置,是过A且与直线AB垂直的直线,与过C平行AB的直线,两直线的交点是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
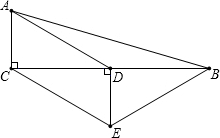 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,垂足为点D,CE∥AD,若AC=2,CE=4.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,垂足为点D,CE∥AD,若AC=2,CE=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y<0 | B. | 0<y<m | C. | m<y<m+4 | D. | y>m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
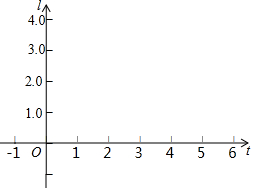 某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:
某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:| t(秒) | 0 | 1 | 2 | 3 | 4 | 5 | … |
| l(米) | 1 | 1.4 | 1.8 | 2.2 | 2.6 | 3.0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
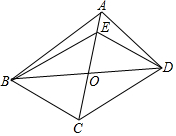 如图,在四边形ABCD中,对角线AC、BD相交于点O,且OB=OD,点E在线段OA上,连接BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是①②(只填写序号).
如图,在四边形ABCD中,对角线AC、BD相交于点O,且OB=OD,点E在线段OA上,连接BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是①②(只填写序号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在Rt△ABC中,∠C=90°,∠A=30°,AB=6,点D,E分别是BC,AB上的动点,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AC上,若△AEB′是等腰三角形,那么CB′的值是3,3$\sqrt{2}$-3,0.
在Rt△ABC中,∠C=90°,∠A=30°,AB=6,点D,E分别是BC,AB上的动点,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AC上,若△AEB′是等腰三角形,那么CB′的值是3,3$\sqrt{2}$-3,0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
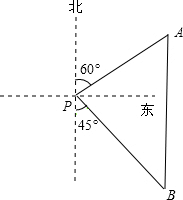 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为102n mile.(结果取整数,参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为102n mile.(结果取整数,参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com