
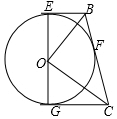
 如图,EG是⊙O的直径,EB,GC,BC分别与⊙O相切于点E,G,F,BE=2,CG=3,求tan∠BCO的值.
如图,EG是⊙O的直径,EB,GC,BC分别与⊙O相切于点E,G,F,BE=2,CG=3,求tan∠BCO的值. 分析 首先利用勾股定理得出直径的长,再利用相似三角形的判定与性质得出△OBE∽△COG,进而得出答案.
解答 解:过点B作BN⊥GC,
∵EB,GC,BC分别与⊙O相切于点E,G,F,
∴∠GEB=∠EGB=∠BNG=90°,
∴四边形EGNB是矩形,
∵BE=2,CG=3,
∴BF=GN=BE=2,GC=FC=3,
∴BC=5,NC=1,
∴BN=$\sqrt{B{C}^{2}-N{C}^{2}}$=2$\sqrt{6}$,
∴EG=2$\sqrt{6}$,
∴EO=OG=$\sqrt{6}$,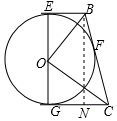
∵EB,GC,BC分别与⊙O相切于点E,G,F,
∴∠EBO=∠OBC,∠BCO=∠OCG,
∵四边形EGNB是矩形,
∴BE∥GC,
∴∠EBC+∠BCG=180°,
∴∠OBC+∠BCO=90°,
∴∠BOC=90°,
∴∠EOB+∠GOC=90°,
∵∠EOB+∠EBO=90°,
∴∠EBO=∠COG,
又∵∠OEB=∠OGC=90°,
∴△OBE∽△COG,
∴$\frac{BO}{CO}$=$\frac{EB}{GO}$=$\frac{2}{\sqrt{6}}$=tan∠BCO,
故tan∠BCO=$\frac{2}{\sqrt{6}}$=$\frac{\sqrt{6}}{3}$.
点评 此题主要考查了切线的性质以及相似三角形的判定与性质等知识,正确得出△OBE∽△COG是解题关键.


科目:初中数学 来源: 题型:解答题
 我们知道,将一个立方体沿某些棱剪开,可以得到它的平面展开图,请画出下面立方体的一种平面展开图,并分别把-3,-2,-1,1,2,3分别填入展开后的六个正方形内,且使原立方体相对面上的两数和为0.
我们知道,将一个立方体沿某些棱剪开,可以得到它的平面展开图,请画出下面立方体的一种平面展开图,并分别把-3,-2,-1,1,2,3分别填入展开后的六个正方形内,且使原立方体相对面上的两数和为0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
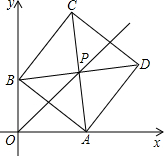 在平面直角坐标系xOy中,边长为2的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C,D都在第一象限.
在平面直角坐标系xOy中,边长为2的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C,D都在第一象限.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com