若方程组$\left\{\begin{array}{l}{3x+2y=m+2}\\{2x+3y=m}\end{array}\right.$的解x与y的和为0.则m的值为( )A．0B．1C．-1D．2 题目和参考答案——青夏教育精英家教网—

19．若方程组$\left\{\begin{array}{l}{3x+2y=m+2}\\{2x+3y=m}\end{array}\right.$的解x与y的和为0，则m的值为（　　）

A．

B．

C．

-1

D．

分析方程组两方程相加表示出x+y，由x+y=0求出m的值即可．

解答解：方程组$\left\{\begin{array}{l}{3x+2y=m+2①}\\{2x+3y=m②}\end{array}\right.$，
①+②得：5（x+y）=2m+2，
即x+y=$\frac{2m+2}{5}$，
由题意得：x+y=0，
∴$\frac{2m+2}{5}$=0，
解得：m=-1，
故选C

点评此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．

练习册系列答案

励耘第1卷中考热身卷浙江各地中考试卷汇编系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

9．

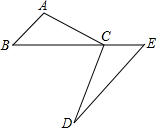如图，C为BE上一点，点A、D分别在BE两侧，AB∥ED，AB=CE，请你添加一个条件，使△ABC≌△CED，你添加的条件是BC=ED，，并写出证明过程．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

10．若m²+m-1=0，则m³+2m²+2017的值为（　　）

A．

2016

B．

2017

C．

2018

D．

2019

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．

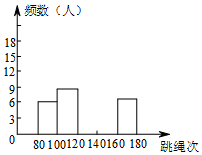体育老师对九年级（9）班50位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图．如下所示：
组别次数x频数和（人数）
第1组80≤x＜1006
第2组100≤x＜1208
第3组120≤x＜140a
第4组140≤x＜16018
第5组160≤x＜1806．
请结合图表完成下列问题：
（1）表中的a=12；
（2）请把频数分布直方图补充完整；
（3）这个样本数据的中位数落在第3组；
（4）若九年级学生一分钟跳绳次数（x）达标要求是：x＜120为不合格；120≤x＜140，为合格；140≤x＜160为良；x≥160为优．根据以上信息，请你给学校或九年级同学提一条合理化建议：加强锻炼，增强体质．．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

14．在等腰直角三角形ABC中，∠BAC=90°，AB=AC，D是斜边BC的中点，连接AD．
（1）如图1，E是AC的中点，连接DE，将△CDE沿CD翻折到△CDE′，连接AE′，当AD=$\sqrt{6}$时，求AE的值．
（2）如图2，在AC上取一点E，使得CE=$\frac{1}{3}$AC，连接DE，将△CDE沿CD翻折到△CDE′，连接AE′交BC于点F，求证：DF=CF．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

4．若方程x-2=0的解也是直线y=（2k-1）x+10与x轴的交点的横坐标，则k的值为（　　）

A．

B．

C．

-2

D．

±2

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．如图1，在平面直角坐标系中，二次函数y=ax²+bx+c的图象经过点A（-1，0），B（4，0）、C（0，$\sqrt{3}$），其中对称轴与x轴交于点E．
（1）求此二次函数的表达式；
（2）如图1，若P为y轴上的一个动点，连接PE，求$\frac{1}{2}$PC+PE的最小值；
（3）如图2，过点C作CF∥AB，交抛物线与点F，M为线段CF的一个动点，连接MO、MB，是否存在一点M，使得sin∠OMB的值最大？若存在，求出此时sin∠OMB的值；若不存在，请说明理由．