
【题目】已知Rt△ABC的斜边AB=6 cm,直角边AC=3 cm.
(1)以C为圆心,2 cm长为半径的圆和AB的位置关系是_________;
(2)以C为圆心,4 cm长为半径的圆和AB的位置关系是_________;
(3)如果以C为圆心的圆和AB相切,则半径长为_________。
 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】(2014贵州黔东南)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠.若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数y=x+![]() (x>0)与y=x+
(x>0)与y=x+![]() (x>0,a>0)的相关性质.
(x>0,a>0)的相关性质.
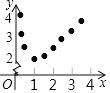
(1)小聪同学对函数y=x+![]() (x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
(x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
x | … |
|
|
| 1 |
| 2 |
| 3 | … |
y | … |
|
|
| 2 |
|
|
|
| … |
(2)请用配方法求函数y=x+![]() (x>0)的最小值;
(x>0)的最小值;
(3)猜想函数y=x+![]() (x>0,a>0)的最小值为 .
(x>0,a>0)的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=AC,P为斜边BC上一点(PB<CP),分别过点B,C作BE⊥AP于点E,CD⊥AP于点D.
(1)求证:AD=BE;
(2)若AE=2DE=2,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
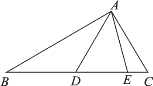
【题目】如图, 在△DAE中, ∠DAE=40°, B、C两点在直线DE上,且∠BAE=∠BEA,∠CAD=∠CDA,则∠BAC的大小是( )
A.100°B.90°C.80°D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
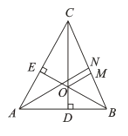
【题目】如图,在△ABC中,CD、BE为高,AN为角平分线,OM平分∠BOC交BC于M.
(1) 若∠BAC=![]() ,求∠BOM;
,求∠BOM;
(2) 求证: OM∥AN.
查看答案和解析>>
科目:初中数学 来源: 题型:
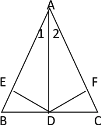
【题目】如图,已知AD是△ABC的中线, DE⊥AB于E, DF⊥AC于F, 且BE=CF, 求证:(1)AD是∠BAC的平分线;(2)AB=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①两点之间,线段最短②![]() ③过
③过![]() 个点可以画无数多条直线,过
个点可以画无数多条直线,过![]() 个点也可以画无数多条直线;④如果
个点也可以画无数多条直线;④如果![]() 与
与![]() 是同类项,那么
是同类项,那么![]() 与
与![]() 互为相反数;⑤珠穆朗玛峰是世界最高峰,它的海拔约为
互为相反数;⑤珠穆朗玛峰是世界最高峰,它的海拔约为![]() 米,这个数字可以用科学记数法表示为
米,这个数字可以用科学记数法表示为![]() ;⑥某商店有两个进价不同的商品都卖了
;⑥某商店有两个进价不同的商品都卖了![]() 元,其中一个盈利
元,其中一个盈利![]() ,另一个亏损
,另一个亏损![]() ,所以这家商店在这次买卖中是赚了
,所以这家商店在这次买卖中是赚了![]() ;其中,正确的是_________.
;其中,正确的是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com