
 于点E,连接BE与AC交于点F.
于点E,连接BE与AC交于点F.| AE |
| BE |
| EF |
| AE |
| AE2 |
| BE |
| 36 |
| 8 |
| 9 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:


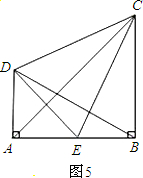
查看答案和解析>>
科目:初中数学 来源: 题型:
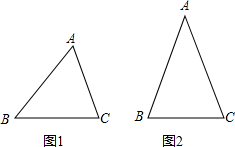
 7、如图,在三角测平架中,AB=AC.在BC的中点D处挂一重锤,让它自然下垂.如果调整架身,使重锤线正好经过点A,那么就能确认BC处于水平位置.这是为什么?
7、如图,在三角测平架中,AB=AC.在BC的中点D处挂一重锤,让它自然下垂.如果调整架身,使重锤线正好经过点A,那么就能确认BC处于水平位置.这是为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论:
小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论: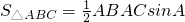 ;
;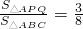 ?
?查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥ AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形, 保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线;
(3)若过A,D,C三点的圆的半径为![]() ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角
形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:福建省模拟题 题型:解答题
 有下面4个结论:
有下面4个结论: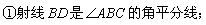 ②
②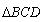 是等腰三角
是等腰三角

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com