
检验:y=3是不是方程2y+5=3-4(1-y)和方程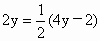 的解?
的解?
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
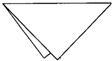 44、(拓展创新)一位女士想买一条方纱巾,有一天她在商店里看到一块漂亮的纱巾,非常想买,但她拿起来看时感觉纱巾不太方,商店老板看她犹豫不决的样子,马上过来拉起一组对角,让女士看另一组对角是否对齐,如图所示,女士还有些疑惑,老板又拉起另一组对角让女士检验,女士终于买下这块纱巾,你认为女士买的这块纱巾是正方形的吗?当时采用什么方法可以检验出来?
44、(拓展创新)一位女士想买一条方纱巾,有一天她在商店里看到一块漂亮的纱巾,非常想买,但她拿起来看时感觉纱巾不太方,商店老板看她犹豫不决的样子,马上过来拉起一组对角,让女士看另一组对角是否对齐,如图所示,女士还有些疑惑,老板又拉起另一组对角让女士检验,女士终于买下这块纱巾,你认为女士买的这块纱巾是正方形的吗?当时采用什么方法可以检验出来?查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x |
| 1 |
| x+10 |
| 1 |
| x+10 |
| 8 |
| x |
| x |
| x+10 |
| 8 |
| x |
| x |
| x+10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
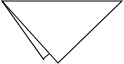
查看答案和解析>>
科目:初中数学 来源:福建省期中题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com