
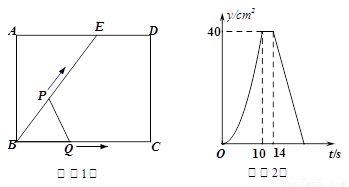
如图(1),E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为 ,已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是(
)
,已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是(
)
A.AE=8
B.当0≤t≤10时,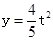
C.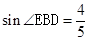
D.当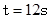 时,△BPQ是等腰三角形
时,△BPQ是等腰三角形
D.
【解析】
试题分析:由图2可知,在点(10,40)至点(14,40)区间,△BPQ的面积不变,因此可推论BC=BE,由此分析动点P的运动过程如下:(1)在BE段,BP=BQ;持续时间10s,则BE=BC=10;y是t的二次函数;(2)在ED段,y=40是定值,持续时间4s,则ED=4;(3)在DC段,y持续减小直至为0,y是t的一次函数.
(1)结论A正确.理由如下:
分析函数图象可知,BC=10cm,ED=4cm,故AE=AD-ED=BC-ED=10-4=6cm;
(2)结论B正确.理由如下:
如图1所示,连接EC,过点E作EF⊥BC于点F,
由函数图象可知,BC=BE=10cm,S△BEC=40=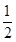 BC•EF=
BC•EF=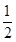 ×10×EF,∴EF=8,
×10×EF,∴EF=8,
∴sin∠EBC=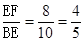 ;
;
(3)结论C正确.理由如下:
如图2所示,过点P作PG⊥BQ于点G,
∵BQ=BP=t,∴y=S△BPQ=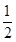 BQ•PG=
BQ•PG=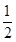 BQ•BP•sin∠EBC=
BQ•BP•sin∠EBC=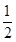 t•t•
t•t•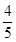 =
=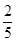 t2.
t2.
(4)结论D错误.理由如下:
当t=12s时,点Q与点C重合,点P运动到ED的中点,设为N,如图3所示,连接NB,NC.
此时AN=8,ND=2,由勾股定理求得:NB=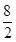 ,NC=
,NC=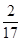 ,
,
∵BC=10,
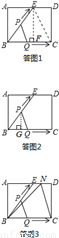
∴△BCN不是等腰三角形,即此时△PBQ不是等腰三角形
考点:动点问题的函数图象.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
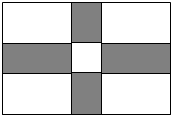 24、学校计划用地砖铺设教学楼前的矩形广场ABCD,已知矩形广场的长为100米,宽为60米图案如图所示:广场四角为矩形,阴影部分为矩形,中心为正方形.阴影部分铺设绿色地砖,其余铺设白色地砖.
24、学校计划用地砖铺设教学楼前的矩形广场ABCD,已知矩形广场的长为100米,宽为60米图案如图所示:广场四角为矩形,阴影部分为矩形,中心为正方形.阴影部分铺设绿色地砖,其余铺设白色地砖.查看答案和解析>>
科目:初中数学 来源: 题型:
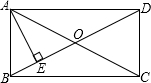 如图所示,四边形ABCD为矩形,点O为对角线的交点,∠BOC=120°,AE⊥BO交BO于点E,AB=4,则AE等于( )
如图所示,四边形ABCD为矩形,点O为对角线的交点,∠BOC=120°,AE⊥BO交BO于点E,AB=4,则AE等于( )A、4
| ||
B、3
| ||
C、2
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com