练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

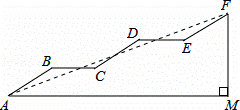
    如图是某通道的侧面示意图，已知AB∥CD∥EF，AM∥BC∥DE，AB=CD=EF，∠BAM=30°，AB=6m．

    （1）求FM的长；

    （2）连接AF，若sin∠FAM=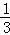，求AM的长．


    解：（1）分别过点B、D、F作BN⊥AM于点N，DG⊥BC延长线于点G，FH⊥DE延长线于点H，

    在Rt△ABN中，

    ∵AB=6m，∠BAM=30°，

    ∴BN=ABsin∠BAN=6×=3m，

    ∵AB∥CD∥EF，AM∥BC∥DE，

    同理可得：DG=FH=3m，

    ∴FM=FH+DG+BN=9m；

     

    （2）在Rt△FAM中，

    ∵FM=9m，sin∠FAM=，

    ∴AF=27m，

    ∴AM==18（m）．

    即AM的长为18m．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    2014年3月份，萧山市区一周空气质量报告中某项污染指数的数据是：61，75 ，61 ，63，50 ，63 ，61，则下列表述错误的是（       ）         

     A．中位数是62        B．众数是61     C．平均数是62     D．极差是25

    查看答案和解析>>

    科目：初中数学 来源： 题型：


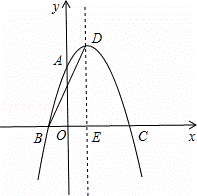
    如图，抛物线y=ax2+2x+c经过点A（0，3），B（﹣1，0），请解答下列问题：

    （1）求抛物线的解析式；

    （2）抛物线的顶点为点D，对称轴与x轴交于点E，连接BD，求BD的长．

    注：抛物线y=ax2+bx+c（a≠0）的顶点坐标是（﹣，）．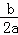

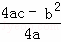    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某校规定：学生的数学学期综合成绩是由平时、期中和期末三项成绩按3：3：4的比例计算所得．若某同学本学期数学的平时、期中和期末成绩分别是90分，90分和85分，则他本学期数学学期综合成绩是　 　分．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解方程：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列计算正确的是（     ）

     A．a2＋a4＝a6   B．2a＋3b＝5ab    C．(a2)3＝a6    D．a6÷a3＝a2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


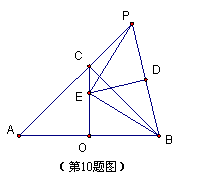
     如图，AB为等腰直角⊿ABC的斜边（AB为定长线段），O为AB的中点，P为AC延长线上的一个动点，线段PB的垂直平分线交线段OC于点E，D为垂足，当P点运动时，给出下列四个结论，其中正确的个数是(   )

    ①E为⊿ABP的外心；②∠PEB=90°；

    ③PC·BE = OE·PB；    ④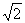CE + PC=．

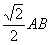    A．1个      B．2个       C．3个       D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，函数y1＝|x|和y2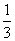＝x＋的图象相交于(－1，1)  (2，2)两点．当y1 ＜y2时，x的取值范围是(　　)

    A．x＜－1      B．－1＜x＜2         C．x＞2        D．x＜－1或x＞2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系中，反比例函数与二次函数y＝k(x2＋x－1)的图象交于点A(1,k)和点B(－1,－k)．

    （1）当k＝－2时，求反比例函数的解析式；

    （2）已知经过原点O的两条直线AB与CD分别与双曲线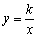（k＞0）交于A、B和C、D，那么AB与CD互相平分，所以四边形ACBD是平行四边形．

    问：平行四边形ABCD能否成为矩形？能否成为正方形？若能，请说明直线AB、CD的位置关系；若不能，请说明理由

    （3）设二次函数的图象的顶点为Q，当△ABQ是以AB为斜边的直角三角形时，求k的值．

    查看答案和解析>>

    同步练习册答案