
【题目】已知关于x的方程x2﹣(2k+1)x+4(k﹣ ![]() )=0
)=0
(1)求证:无论k取何值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长a=4,另两边b、c恰好是这个方程的两个根,求△ABC的周长.
【答案】
(1)证明:△=(2k+1)2﹣4×4(k﹣ ![]() )
)
=4k2+4k+1﹣16k+8,
=4k2﹣12k+9
=(2k﹣3)2,
∵(2k﹣3)2≥0,即△≥0,
∴无论k取何值,这个方程总有实数根;
(2)解:当b=c时,△=(2k﹣3)2=0,解得k= ![]() ,方程化为x2﹣4x+4=0,解得b=c=2,而2+2=4,故舍去;
,方程化为x2﹣4x+4=0,解得b=c=2,而2+2=4,故舍去;
当a=b=4或a=c=4时,把x=4代入方程得16﹣4(2k+1)+4(k﹣ ![]() )=0,解得k=
)=0,解得k= ![]() ,方程化为x2﹣6x+8=0,解得x1=4,x2=2,即a=b=4,c=2或a=c=4,b=2,
,方程化为x2﹣6x+8=0,解得x1=4,x2=2,即a=b=4,c=2或a=c=4,b=2,
所以△ABC的周长=4+4+2=10.
【解析】(1)先计算判别式的值得到△=4k2﹣12k+9,配方得到△=(2k﹣3)2 , 根据非负数的性质易得△≥0,则根据判别式的意义即可得到结论;(2)分类讨论:当b=c时,则△=(2k﹣3)2=0,解得k= ![]() ,然后解方程得到b=c=2,根据三角形三边关系可判断这种情况不符号条件;当a=b=4或a=c=4时,把x=4代入方程可解得k=
,然后解方程得到b=c=2,根据三角形三边关系可判断这种情况不符号条件;当a=b=4或a=c=4时,把x=4代入方程可解得k= ![]() ,则方程化为x2﹣6x+8=0,解得x1=4,x2=2,所以a=b=4,c=2或a=c=4,b=2,然后计算△ABC的周长.
,则方程化为x2﹣6x+8=0,解得x1=4,x2=2,所以a=b=4,c=2或a=c=4,b=2,然后计算△ABC的周长.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC﹣BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=4AD,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家、食堂、图书馆依次在同一条直线上,小明从家去食堂吃早餐,接着云图书馆读报,然后回家。如图反映了这个过程,小明离家的距离与时间之间的对应关系,下列说法错误的是( )
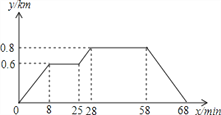
A. 小明从家到食堂用了8min B. 小明家离食堂0.6km,食堂离图书馆0.2km
C. 小明吃早餐用了30min,读报用了17min D. 小明从图书馆回家的平均速度为0.08km/min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划从某苗木基地购进A、B两咱树苗共200棵绿化校园。已知购买了3棵A种树苗和5棵B种树苗共需700元;购买2棵A种树苗和1棵B种树苗共需280元.
(1)每棵A种树苗、B种树苗各需多少元?
(2)学校除支付购买树苗的费用外,平均每棵树苗还需支付运输及种植费用20元。设学校购买B种树苗x棵,购买两种树苗及运输、种植所需的总费用为y元,求y与x的函数关系;
(3)在(2)的条件下,若学校用于绿化的总费用在22400元限额内,且购买A种树苗的数量不少于B种树苗的数量,请给出一种费用最省的方案,并求出该方案所需的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+ ![]() 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 . 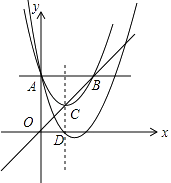
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 为直线
为直线![]() 上一点,以
上一点,以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 平分
平分![]() .
.
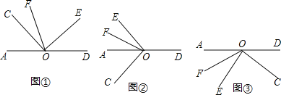
![]() 如图①,
如图①,![]() 与
与![]() 的数量关系为________,
的数量关系为________,![]() 和
和![]() 的数量关系为_________;
的数量关系为_________;
![]() 若将
若将![]() 绕点
绕点![]() 旋转至图②的位置,
旋转至图②的位置,![]() 依然平分
依然平分![]() ,请写出
,请写出![]() 和
和![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
![]() 若将
若将![]() 绕点
绕点![]() 旋转至图③的位置,射线
旋转至图③的位置,射线![]() 依然平分
依然平分![]() ,请直接写出
,请直接写出![]() 和
和![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com