
分析 (1)由|a-b|表示数轴上数a的点与数b的点的距离可知|x-1|表示数轴上表示x的点与数1的点的距离;
(2)当x=2时,|x-1|+2|x-2|+|x-4|可转化为数轴上表示2的点到1和4的距离之和;
(3)可分为x≤1,1<x≤2,x>2三种情况进行化简计算.
解答 解:(1)|x-1|表示数轴表示数x的点与表示数1的点的距离;
故答案为:数轴表示数x的点与表示数1的点的距离.
(2)当x=2时,|x-1|+2|x-2|+|x-4|可转化为数轴上表示2的点到1和4的距离之和,
∴当x=2时,|x-1|+2|x-2|+|x-4|的最小值为3;
(3)当x≤1时,1-x+2(2-x)=8.
解得:x=-1.
当1<x≤2时,x-1+2(2-x)=8,
解得:x=-5(不合题意).
当x>2时,x-1+2(x-2)=8,
解得:x=$\frac{13}{3}$.
综上所述,x的值为-1或$\frac{13}{3}$
点评 本题主要考查的是绝对值、数轴、解含绝对值的方程,分类讨论是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | y的值随着x的增大而减小 | |
| B. | 图象是双曲线,是中心对称图形且是轴对称 | |
| C. | 当x>1时,0<y<1 | |
| D. | 图象可能与坐标轴相交 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
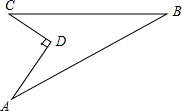 如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+b<0 | B. | a-b<0 | C. | a•b<0 | D. | (-$\frac{b}{a}$)3>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
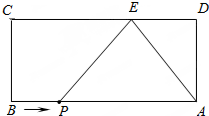 如图,已知正方形ABCD,AB=8,AD=4,E为CD边上一点,CE=5.
如图,已知正方形ABCD,AB=8,AD=4,E为CD边上一点,CE=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com