
【题目】已知二次函数![]() 自变量
自变量![]() 的值和它对应的函数值
的值和它对应的函数值![]() 如下表所示:
如下表所示:
|
| 0 | 1 | 2 | 3 | 4 |
|
|
| 3 | 0 | -1 | 0 |
|
|
(1)请写出该二次函数图像的开口方向、对称轴、顶点坐标和![]() 的值;
的值;
(2)设该二次函数图像与![]() 轴的左交点为
轴的左交点为![]() ,它的顶点为
,它的顶点为![]() ,该图像上点
,该图像上点![]() 的横坐标为4,求
的横坐标为4,求![]() 的面积.
的面积.
【答案】(1)开口向上,对称轴:![]() ;顶点
;顶点![]() ,
,![]() ;(2)3
;(2)3
【解析】
(1)根据表格中的数据和二次函数的性质,可以得到该二次函数图象的开口方向、对称轴、顶点坐标和m的值;
(2)根据表格中的数据和题意,可以写出点B、点A和点C的坐标,再求出直线AC和x轴的交点,即可得到△ABC的面积.
(1)由表格可知,
该函数有最小值,当x=2时,y=-1,当x=4和x=0时的函数值相等,则m=3,
即该二次函数图象的开口方向向上,对称轴是直线x=2,顶点坐标为(2,-1),m的值是3;
(2)由题意可得,
点B的坐标为(1,0),点A的坐标为(2,-1),点C的坐标为(4,3),
设直线AC的函数解析式为y=kx+b,
![]() ,得
,得![]() ,
,
所以直线AC的函数解析式为y=2x-5,
当y=0时,0=2x-5,得x=2.5,
则直线AC与x轴的交点为(2.5,0),
故△ABC的面积是:![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】某果园有100棵橙子树,平均每棵结600个橙子.现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就要减少.根据经验估计,每增种1棵树,平均每棵树就少结5个橙子.设果园增种x棵橙子树,果园橙子的总产量为y个.
(1)求y与x之间的关系式;
(2)增种多少棵橙子树,可以使橙子的总产量在60 420个以上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:![]() 的坡面AD走了200
的坡面AD走了200![]() 米到D处,此时在D处测得山顶B的仰角为60°,则山高BC=_____米(结果保留根号).
米到D处,此时在D处测得山顶B的仰角为60°,则山高BC=_____米(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
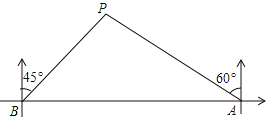
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有3个标有1,2,3的小球,它们的形状,大小完全相同,李强从布袋中随机取出一个小球,记下数字为x,然后放回袋中搅匀,王芳再从袋中随机取出一个小球,记下数字为y,这样确定了点M的坐标(x,y).
(1)用列表或画树状图(只选其中一种)的方法表示出点M所有可能的坐标;
(2)求点M(x,y)在函数y=x2图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x+b与y轴交于点B(0,﹣3),与反比例函数y=
x+b与y轴交于点B(0,﹣3),与反比例函数y=![]() (x>0)的图象交于点A,与x轴交于点C,BC=3AC
(x>0)的图象交于点A,与x轴交于点C,BC=3AC
(1)求反比例函数的解析式;
(2)若P是y轴上一动点,M是直线AB上方的反比例函数y=![]() (x>0)的图象上一动点,直线MN⊥x轴交直线AB于点N,求△PMN面积的最大值.
(x>0)的图象上一动点,直线MN⊥x轴交直线AB于点N,求△PMN面积的最大值.
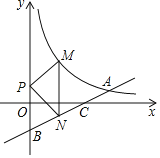
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏).设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.
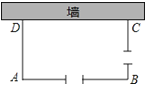
(1)若所用铁栅栏的长为40米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() ,直线
,直线![]()
(1)当m=0时,若直线![]() 经过此抛物线的顶点,求b的值
经过此抛物线的顶点,求b的值
(2)将此抛物线夹在![]() 之间的部分(含交点)图象记为
之间的部分(含交点)图象记为![]() ,若
,若![]() ,
,
①判断此抛物线的顶点是否在图象![]() 上,并说明理由;
上,并说明理由;
②图象![]() 上是否存在这样的两点:
上是否存在这样的两点:![]() ,其中
,其中![]() ?若存在,求相应的
?若存在,求相应的![]() 和
和![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com