
 如图,在直角坐标系中,A(0,4),B(-2,0),C(2,0).
如图,在直角坐标系中,A(0,4),B(-2,0),C(2,0).分析 (1)过点A作射线AD∥x轴,过点C以CA长度为半径作弧,交射线AD与点D,连接CD即可;
(2)过点C作CE⊥AD与点E,则四边形AOCE为矩形,由此可得出AE=OC,再根据等腰三角形的性质结合点B、C的坐标即可得出AD=BC,由AD∥x轴即可证出四边形ABCD为平行四边形;
(3)由直线的解析式可找出直线于x轴的交点坐标,在AD边上取DN=BM,则点N(3,4),将点D的坐标代入直线解析式中即可求出k值.
解答 解:(1)过点A作射线AD∥x轴,过点C以CA长度为半径作弧,交射线AD与点D,连接CD,如图1所示.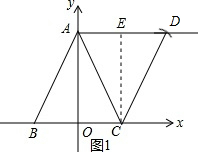
(2)在图1中,过点C作CE⊥AD与点E,
∵CA=CD,
∴AE=DE.
∵AO∥CE,∠AOC=90°,
∴四边形AOCE为矩形,
∴AE=OC.
∵B(-2,0),C(2,0),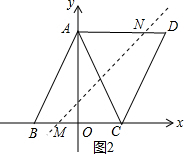
∴BC=2OC=AD.
∵AD∥x轴,
∴四边形ABCD为平行四边形.
故答案为:平行四边形.
(3)∵y=kx+k=k(x+1),
∴直线过点M(-1,0),
∴BM=1.
在AD边上取DN=BM,
∵AD=BC=2-(-2),DN=BM=1,
∴AN=3,
∴点N(3,4).
将N(3,4)代入y=kx+k,
4=3k+k,解得:k=1.
故答案为:1.
点评 本题考查了一次函数图象与几何变换、平行四边形的判定依据待定系数法求一次函数解析式,解题的关键是:(1)通过画弧截取CD=CA;(2)利用“一组对边平行且相等的四边形是平行四边形”证出四边形ABCD为平行四边形;(3)根据点N的坐标利用待定系数法求出k值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
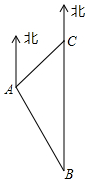 如图,某渔船航行至B处时,侧得一海岛位于B处的正北方向20(1+$\sqrt{3}$)海里的C处,为了防止意外,渔船请求A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位子B的北偏西300的方向上,求A,C之间的距离.
如图,某渔船航行至B处时,侧得一海岛位于B处的正北方向20(1+$\sqrt{3}$)海里的C处,为了防止意外,渔船请求A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位子B的北偏西300的方向上,求A,C之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com