
分析 根据题意求出顶点横坐标,确定出顶点坐标,设出顶点形式,把(-2,0)代入求出解析式即可.
解答 解:根据题意知抛物线顶点的横坐标为x=$\frac{-2+6}{2}=2$,纵坐标为-$\frac{9}{2}$,
即顶点坐标为(2,-$\frac{9}{2}$),
设抛物线解析式为:y=a(x-2)2-$\frac{9}{2}$,
将点(-2,0)代入,得:16a-$\frac{9}{2}$=0,
解得:a=$\frac{9}{32}$,
故抛物线解析式为:y=$\frac{9}{32}$(x-2)2-$\frac{9}{2}$.
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
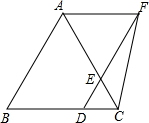 已知△ABC为边长为6的等边三角形,D、E分别在边BC、AC上,且CD=CE=x,连接
已知△ABC为边长为6的等边三角形,D、E分别在边BC、AC上,且CD=CE=x,连接查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
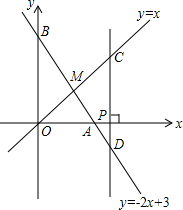 如图,已知函数y=-2x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.在X轴上有一点P(a,0)(其中a>1),过点P作x轴的垂线,分别交函数y=x和y=-2x+3的图象于点C、D.若CD=3,求a的值.
如图,已知函数y=-2x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.在X轴上有一点P(a,0)(其中a>1),过点P作x轴的垂线,分别交函数y=x和y=-2x+3的图象于点C、D.若CD=3,求a的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年度 | 2001 | 2002 | 2003 | 2004 |
| 投入技术改进资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y=kx+b,在x=0时的值为4,在x=-1时的值为-2,
已知一次函数y=kx+b,在x=0时的值为4,在x=-1时的值为-2,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com