
【题目】(1)数学爱好者小森偶然阅读到这样一道竞赛题:
一个圆内接六边形ABCDEF,各边长度依次为 3,3,3,5,5,5,求六边形ABCDEF的面积.
小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理,将六边形进行分割重组,得到图③.可以求出六边形ABCDEF的面积等于 .
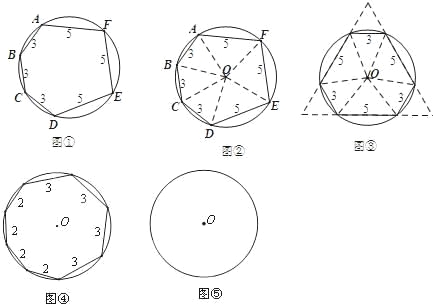
(2)类比探究:一个圆内接八边形,各边长度依次为2,2,2,2,3,3,3,3.求这个八边形的面积.请你仿照小森的思考方式,求出这个八边形的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)如图③,利用六边形ABCDEF每次绕圆心O旋转120°都和原来的图形重合可判断△MNQ为等边三角形,△MAF、△NBC和△QDE都是等边三角形,然后根据等边三角形的面积公式求解;
(2)先画出分割重组的图形,如图⑤,利用八边形ABCDEFGH为轴对称图形,每次绕圆心O旋转90°都和原来的图形重合,可判断四边形PQMN为正方形,△PAB、△GCD、△MEF、△NHG都是等腰直角三角形,根据根据正方形的性质和等腰直角三角形的性质求解.
试题解析:(1)如图③,∵六边形ABCDEF为轴对称图形,每次绕圆心O旋转120°都和原来的图形重合,∴△MNQ为等边三角形,△MAF、△NBC和△QDE都是等边三角形,
∴NQ=3+5+3=11,
∴六边形ABCDEF的面积=S△MNQ﹣3S△AMN
=![]() ×112﹣3×
×112﹣3×![]() ×32
×32
=![]() ;
;
故答案为![]() .
.
(2)如图⑤,∵八边形ABCDEFGH为轴对称图形,每次绕圆心O旋转90°都和原来的图形重合,
∴四边形PQMN为正方形,△PAB、△GCD、△MEF、△NHG都是等腰直角三角形,
∴PA=![]() AB=
AB=![]() ,PN=
,PN=![]() +3+
+3+![]() =3+2
=3+2![]() ,
,
∴这个八边形的面积=(3+2![]() )2﹣4×
)2﹣4×![]() ×
×![]() ×
×![]() =9+12
=9+12![]() +8﹣4=13+12
+8﹣4=13+12![]() .
.



 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】若将函数y=2x2的图象向右平行移动1个单位,再向上平移3个单位,得到的抛物线是( )
A.y=2(x+5)2﹣1B.y=2(x+5)2+1
C.y=2(x﹣1)2+3D.y=2(x+1)2﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=(x﹣1)2+3关于x轴对称的抛物线的解析式是( )
A.y=﹣(x﹣1)2+3B.y=(x+1)2+3
C.y=(x﹣1)2﹣3D.y=﹣(x﹣1)2﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
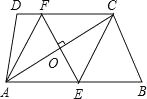
【题目】如图,在梯形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB、CD于点E、F,连接CE、AF.
(1)求证:四边形AECF是菱形;
(2)若EF=4,tan∠OAE=![]() ,求四边形AECF的面积.
,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区新教师招聘中,九位评委独立给出分数,得到一列数.若去掉一个最高分和一个最低分,得到一列新数,那么这两列数的相关统计量中,一定相等的是( )
A.方差B.众数C.中位数D.平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月3日至3月15日,中国进入“两会时间”,根据数据统计显示,2019年全国两会热点传播总量达829.8万条,其中数据“829.8万”用科学记数法表示为( )
A. 8.298×107B. 82.98×105C. 8.298×106D. 0.8298×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学规定学生的学期体育总评成绩满分为100分,其中平均成绩占20%,期中考试成绩占30%,期末考试成绩占50%,小彤的三项成绩(百分制)依次为95,90,88,则小彤这学期的体育总评成绩为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
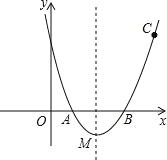
【题目】如图,抛物线y=![]() 过点C(4,3),交x轴于A,B两点(点A在点B的左侧).
过点C(4,3),交x轴于A,B两点(点A在点B的左侧).
(1)求抛物线的解析式,并写出顶点M的坐标;
(2)连接OC,CM,求tan∠OCM的值;
(3)若点P在抛物线的对称轴上,连接BP,CP,BM,当∠CPB=∠PMB时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com