
【题目】已知直角△ABC,∠BAC=90°,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF连接EF

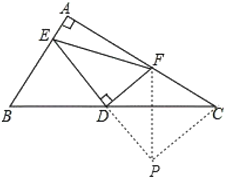
(1)如图1,求证:∠BED=∠AFD;
(2)求证:BE2+CF2=EF2;
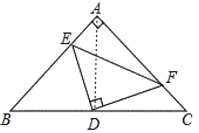
(3)如图2,当∠ABC=45°,若BE=12,CF=5,求△DEF的面积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)利用四边形内角和得出∠AED+∠AFD=180°,再根据补角的性质即可得;
(2)延长ED至点P,使ED=DP,构造全等三角形,利用全等三角形的性质得到直角三角形,由勾股定理及等量代换可得;
(3)由(2)结论求EF长,再通过全等证明DE=DF,由面积公式求解.
解:(1)∵DE⊥DF,
∴∠EDF=90°,
∵∠BAC=90°,
∴∠AED+∠AFD=180°,
∵∠AED+∠BED=180°,
∴∠BED=∠AFD;
(2)如图,
延长ED至点P,使ED=DP,连接CP,EP,
∵FD⊥EP,
∴FD为EP的垂直平分线,
∴EF=FP,
∵ED=DP, ∠EDB=∠CDP,BD=CD,
∴△EDB≌PDC,
∴EB=CP, ∠B=∠DCP,
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠DCP+∠ACB=90°,
即∠ACP=90°,
由勾股定理得,CP2+CF2=FP2,
∴BE2+CF2=EF2;
(3)如图,∵BE2+CF2=EF2
∴52+122=EF2,
∴EF=13,
∵△ABC是等腰直角三角形,BD=CD,
∴AD⊥BC, ∴∠ADC=90°, ∠BAD=∠B=∠C=45°,
∵∠EDF=90°
∴∠ADE=∠CDF,
∴△ADE≌CDF,
∴DE =DF=![]() ,
,
∴S△DEF=![]() .
.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
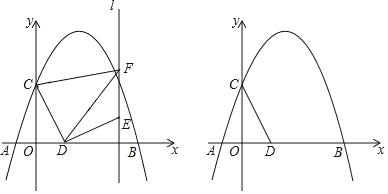
【题目】如图,抛物线y=﹣![]() +bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
+bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
(1)求抛物线解析式;
(2)若线段DE是CD绕点D顺时针旋转90°得到,求线段DF的长;
(3)若线段DE是CD绕点D旋转90°得到,且点E恰好在抛物线上,请求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个三角形中,如果一个角是另一个角的2倍,我们称这种三角形为倍角三角形.如图1,倍角△ABC中,∠A=2∠B,∠A、∠B、∠C的对边分别记为a,b,c,倍角三角形的三边a,b,c有什么关系呢?让我们一起来探索.

(1)我们先从特殊的倍角三角形入手研究.请你结合图形填空:
三三角形角形 | 角的已知量 |
|
|
图2 | ∠A=2∠B=90° | ||
图3 | ∠A=2∠B=60° |
(2)如图4,对于一般的倍角△ABC,若∠CAB=2∠CBA,∠CAB、∠CBA、∠C的对边分别记为a,b,c,a,b,c,三边有什么关系呢?请你作出猜测,并结合图4给出的辅助线提示加以证明;
(3)请你运用(2)中的结论解决下列问题:若一个倍角三角形的两边长为5,6,求第三边长.(直接写出结论即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款工艺品,每件成本![]() 元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是![]() 元时,每天的销售量是
元时,每天的销售量是![]() 件,若销售单价每降低
件,若销售单价每降低![]() 元,每天就可多售出
元,每天就可多售出![]() 件,但要求销售单价不得低于
件,但要求销售单价不得低于![]() 元.如果降价后销售这款工艺品每天能盈利
元.如果降价后销售这款工艺品每天能盈利![]() 元,那么此时销售单价为多少元?
元,那么此时销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
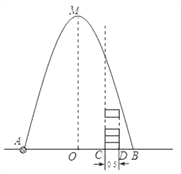
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com