
分析 可设定点D(0,c),过D的直线与抛物线交于E、F两点,分别设出E、F的坐标,可表示出直线CE、CF的斜率,根据两直线垂直,结合一元二次方程根与系数的关系可得到关于c的方程,可求得c的值.
解答 解:∵抛物线y=$\frac{1}{4}$x2-4的对称轴是y轴,
∴设定点D(0,c),过点D的直线为y=ax+c,
设过D的直线与抛物线交于E、F两点,设E(xE,yE),F(xF,yF)
则yE=$\frac{1}{4}$xE-4,yF=$\frac{1}{4}$xF-4,
由y=$\frac{1}{4}$x2-4可知顶点C(0,-4),
∴kCE=$\frac{{y}_{E}+4}{{x}_{E}}$=$\frac{{{\frac{1}{4}x}_{E}}^{2}}{{x}_{E}}$=$\frac{1}{4}$xE,
同理kCF=$\frac{1}{4}$xF,
∵直线CE、CF互相垂直,
∴kCE•kCF=-1,即$\frac{1}{4}$xE•$\frac{1}{4}$xF=-1,
∴xE•xF=-16,
联立过D的直线和抛物线解析式$\left\{\begin{array}{l}{y=ax+c}\\{y=\frac{1}{4}{x}^{2}-4}\end{array}\right.$,消去y可得$\frac{1}{4}$x2-ax-4-c=0,
由题意可知xE和xF是该方程的两根,
∴xE•xF=$\frac{-4-c}{\frac{1}{4}}$=-16-4c,
∴-16-4c=-16,解得c=0,
∴D点坐标为(0,0),
即存在满足条件的D点.
点评 本题主要考查二次函数与x轴的交点问题,由直线相互垂直得关于D点坐标的方程是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒$\sqrt{2}$个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
在直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒$\sqrt{2}$个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠DCB=60°,AD=2$\sqrt{3}$,BC=6$\sqrt{3}$,点G是线段AB中点,点F在线段BC上,连接GF,将线段GF绕点G逆时针旋转60°,得到线段GE,GE交CD于点H,连结DE,且DE⊥DC,则HE的长为$\frac{8\sqrt{21}}{3}$.
如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠DCB=60°,AD=2$\sqrt{3}$,BC=6$\sqrt{3}$,点G是线段AB中点,点F在线段BC上,连接GF,将线段GF绕点G逆时针旋转60°,得到线段GE,GE交CD于点H,连结DE,且DE⊥DC,则HE的长为$\frac{8\sqrt{21}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向北走120米 | B. | 向北走50米 | C. | 向北走40米 | D. | 向北走30米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{2(x-1)≥x-4}\\{\frac{x+7}{2}>x+2}\end{array}\right.$,并把不等式组的解集表示在数轴上.
解不等式组:$\left\{\begin{array}{l}{2(x-1)≥x-4}\\{\frac{x+7}{2}>x+2}\end{array}\right.$,并把不等式组的解集表示在数轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
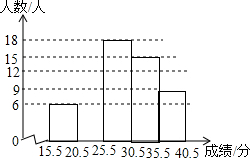 某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).
某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).| 分组 | 频数 | 频率 |
| 15.5~20.5 | 6 | 0.10 |
| 20.5~25.5 | a | 0.20 |
| 25.5~30.5 | 18 | 0.30 |
| 30.5~35.5 | 15 | b |
| 35.5~40.5 | 9 | 0.15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com