
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
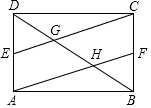 矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
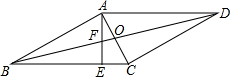 如图,在平行四边形ABCD中,对角线AC、BD交于点O、AC⊥AB、∠ABC=30°,过点A作AE⊥BC于点E,交BD于点F,则$\frac{AF}{AO}$=$\frac{4\sqrt{3}}{7}$.
如图,在平行四边形ABCD中,对角线AC、BD交于点O、AC⊥AB、∠ABC=30°,过点A作AE⊥BC于点E,交BD于点F,则$\frac{AF}{AO}$=$\frac{4\sqrt{3}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
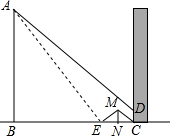 阳光明媚的一天,小华和小红两人想利用自己所学知识测量楼前旗杆的高度,某一时刻旗杆AB的影子一部分在地面上,另一部分在数学楼的墙面上高度记为CD,同一时刻小华蹲在地面N处,小华的影子刚好到达墙角C处;小红在小华与旗杆之间的直线BN上平放一平面镜,经过不断调整,直到小华能在镜子中看到旗杆的顶部,记平面镜的位置为E(忽略平面镜的高度),小华蹲着的高度记为MN(忽略眼晴到头顶的距离),且小华蹲在地面上的高度一直保持不变,此时小红测得BE=12.51米,EN=1.09米,NC=1.4米,CD=1米,求旗杆的高度.(结果精确到0.1米)
阳光明媚的一天,小华和小红两人想利用自己所学知识测量楼前旗杆的高度,某一时刻旗杆AB的影子一部分在地面上,另一部分在数学楼的墙面上高度记为CD,同一时刻小华蹲在地面N处,小华的影子刚好到达墙角C处;小红在小华与旗杆之间的直线BN上平放一平面镜,经过不断调整,直到小华能在镜子中看到旗杆的顶部,记平面镜的位置为E(忽略平面镜的高度),小华蹲着的高度记为MN(忽略眼晴到头顶的距离),且小华蹲在地面上的高度一直保持不变,此时小红测得BE=12.51米,EN=1.09米,NC=1.4米,CD=1米,求旗杆的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
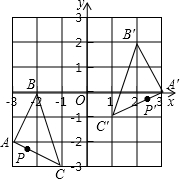 如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )
如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )| A. | (-m,n+2) | B. | (-m,n-2) | C. | (-m-2,-n) | D. | (-m-2,n-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
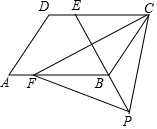 如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com