
分析 (1)去括号然后合并同类项即可解答本题;
(2)根据有理数的加法和减法可以解答本题;
(3)先去绝对值符号,然后根据有理数的减法可以解答本题;
(4)先去括号,再根据有理数的加法和减法可以解答本题.
解答 解:(1)(-2$\frac{3}{4}$)+1$\frac{3}{4}$+1$\frac{1}{3}$+(-5$\frac{1}{3}$)
=[(-2$\frac{3}{4}$)+(-5$\frac{1}{3}$)]+[1$\frac{3}{4}$+1$\frac{1}{3}$]
=(-8)+3
=-5;
(2)0-29.8-17.5+16.5-2.2+7.5
=(-29.8-17.5-2.2)+(16.5+7.5)
=(-49.5)+24
=-25.5;
(3)|-3$\frac{1}{2}$-(-2$\frac{1}{3}$)|-(|-5$\frac{1}{3}$|-|-$\frac{3}{4}$|)
=|$-3\frac{1}{2}+2\frac{1}{3}$|-($5\frac{1}{3}-\frac{3}{4}$)
=$1\frac{1}{6}-4\frac{7}{12}$
=$-3\frac{5}{12}$;
(4)[1$\frac{3}{5}$-(-3.6+5.2)+4.2]-(-1$\frac{1}{2}$)
=[1.6-1.6+4.2]+1.5
=4.2+1.5
=5.7.
点评 本题考查有理数的加减混合运算,解题的关键是明确有理数混合运算的计算方法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是(-4,3),B(-6,0),O是原点,点M是OB边上异于O,B的一动点,过点M作MN∥AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点M(x,0).
如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是(-4,3),B(-6,0),O是原点,点M是OB边上异于O,B的一动点,过点M作MN∥AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点M(x,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
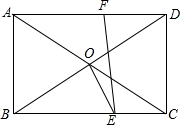 如图,矩形ABCD的两条对角线AC,BD相交于点O,夹角为60°,点E,F分别在BC,AD上,四边形ABEF是正方形,连接OE,则∠BOE=75°.
如图,矩形ABCD的两条对角线AC,BD相交于点O,夹角为60°,点E,F分别在BC,AD上,四边形ABEF是正方形,连接OE,则∠BOE=75°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BD平分∠ABC交AC于点D,DE∥AB交BC于E,过E作EF∥BD交AC于F.
如图,BD平分∠ABC交AC于点D,DE∥AB交BC于E,过E作EF∥BD交AC于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com